题目内容
在一次数学探究性学习活动中,某学习小组要制作一个圆锥体模型,操作规则是:在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二.(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切)
(1)请说明方案一不可行的理由;
(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由.

【答案】
解:(1)理由如下:
∵扇形的弧长=16× =8π,圆锥底面周长=2πr,∴圆的半径为4cm.
=8π,圆锥底面周长=2πr,∴圆的半径为4cm.
由于所给正方形纸片的对角线长为 cm,而制作这样的圆锥实际需要正方形纸片的对角线长为
cm,而制作这样的圆锥实际需要正方形纸片的对角线长为 cm,
cm, ,
,
∴方案一不可行.
(2)方案二可行.求解过程如下:
设圆锥底面圆的半径为rcm,圆锥的母线长为Rcm,则
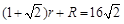 , ①
, ①
 . ②
. ②
由①②,可得 ,
, . 故所求圆锥的母线长为
. 故所求圆锥的母线长为 cm,底面圆的半径为
cm,底面圆的半径为 cm.
cm.
【解析】(1)首先根据扇形的弧长公式及圆锥底面周长求出底面圆的半径,再比较所给正方形纸片的对角线与制作这样的圆锥实际需要正方形纸片的对角线长即可得到结论;
(2)先设出圆锥底面圆的半径及圆锥的母线长,再根据正方形的性质及圆锥底面周长公式列出方程组,即可得到结果。

练习册系列答案
相关题目



