题目内容
【题目】如图，四边形ABCD中，∠BAD=∠BCD=90°，AB=AD= 
，CD=2，BC=4，则AC= 
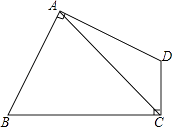
【答案】3 
【解析】解：过A作AE⊥BC，作AF⊥CD，交CD的延长线于点F，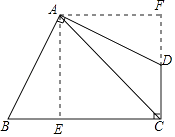 
∵∠AEC=∠AFC=∠ECF=90°，
∴四边形AECF为矩形，
∴∠EAF=90°，
∵∠BAD=90°，
∴∠BAE+∠EAD=∠FAD+∠EAD=90°，
∴∠DAF=∠BAE，
在△ABE和△ADF中，
∵ 
，
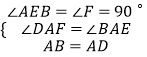∴△ABE≌△ADF（AAS），
∴AE=AF，
∴四边形AECF是正方形
∴AF=EC，
设BE=x，则EC=AF=AE=4﹣x，
∵AB2=AE2+BE2 ，
∴（ 
）2=（4﹣x）2+x2 ， 解得：x=1或x=3（舍），
∴AE=EC=3，
∴AC=3 ，
所以答案是：3 ．
练习册系列答案
相关题目
