题目内容
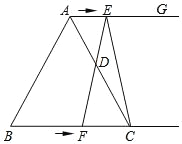
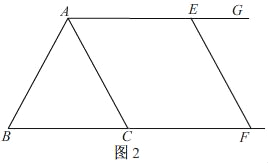
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;
②当t为 s时,△ACE的面积是△ACF的面积的2倍.
【答案】(1)证明见解析;(2)①8;②![]() 或
或![]() .
.
【解析】
(1)判断出△ADE≌△CDF得出AE=CF,即可得出结论;
(2)①先求出AC=BC=8,进而判断出AE=CF=AC=8,即可得出结论;
②先判断出△ACE和△ACF的边AE和CF上的高相等,进而判断出AE=2CF,再分两种情况,建立方程求解即可得出结论.
解:(1)如图1.
∵AG∥BC,
∴∠EAC=∠FCA,∠AED=∠CFD.
∵EF经过AC边的中点D,
∴AD=CD,
∴△ADE≌△CDF(AAS),
∴AE=CF.
∵AE∥FC,
∴四边形AFCE是平行四边形;
(2)①如图2.
∵△ABC是等边三角形,
∴AC=BC=8.
∵四边形ACFE是菱形,
∴AE=CF=AC=BC=8,且点F在BC延长线上,由运动知,AE=t,BF=2t,
∴CF=2t﹣8,t=8,将t=8代入CF=2t﹣8中,
得CF=8=AC=AE,符合题意,即:t=8秒时,四边形ACFE是菱形.
故答案为:8;
②设平行线AG与BC的距离为h,
∴△ACE边AE上的高为h,△ACF的边CF上的高为h.
∵△ACE的面积是△ACF的面积的2倍,
∴AE=2CF,当点F在线段BC上时(0<t<4),CF=8﹣2t,AE=t,
∴t=2(8﹣2t),
∴![]()
当点F在BC的延长线上时(t>4),CF=2t﹣8,AE=t,
∴t=2(2t﹣8),
∴![]()
即:t=![]() 秒或
秒或![]() 秒时,△ACE的面积是△ACF的面积的2倍.
秒时,△ACE的面积是△ACF的面积的2倍.
故答案为:![]() 或
或![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案