题目内容
 如图所示,⊙M与x轴相切于原点,平行于y轴的直线交圆于P,Q两点,P点在Q点的下方,若P点坐标是(2,1),则圆心M的坐标是
如图所示,⊙M与x轴相切于原点,平行于y轴的直线交圆于P,Q两点,P点在Q点的下方,若P点坐标是(2,1),则圆心M的坐标是
- A.(0,3)
- B.(0,
 )
) - C.(0,2)
- D.(0,
 )
)
B
分析:连接MP,过M作MA⊥PQ于A,设⊙M的半径为R,所以MP=R,PA=R-1,MA=PB=2,根据勾股定理则有:MP2=MA2+PA2,即可求得R= .
.
解答: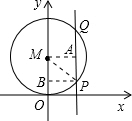 解:连MP,过M作MA⊥PQ于A,则PB=MA=2,
解:连MP,过M作MA⊥PQ于A,则PB=MA=2,
设⊙M的半径为R,则MP2=MA2+PA2,
即R2=22+(R-1)2,
解得R= ,
,
故选B.
点评:解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.
分析:连接MP,过M作MA⊥PQ于A,设⊙M的半径为R,所以MP=R,PA=R-1,MA=PB=2,根据勾股定理则有:MP2=MA2+PA2,即可求得R=
 .
.解答:
 解:连MP,过M作MA⊥PQ于A,则PB=MA=2,
解:连MP,过M作MA⊥PQ于A,则PB=MA=2,设⊙M的半径为R,则MP2=MA2+PA2,
即R2=22+(R-1)2,
解得R=
 ,
,故选B.
点评:解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.

练习册系列答案
相关题目
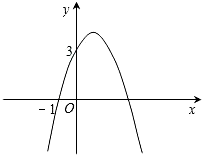 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).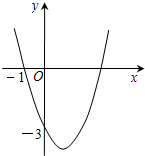 点坐标为(0,-3).
点坐标为(0,-3). (2012•天门)已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有( )
(2012•天门)已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有( ) (2012•思明区质检)已知二次函数y=ax2+bx+c(a<0)的部分图象如图所示,抛物线与x轴的一个交点坐标为(3,0),对称轴为直线x=1.
(2012•思明区质检)已知二次函数y=ax2+bx+c(a<0)的部分图象如图所示,抛物线与x轴的一个交点坐标为(3,0),对称轴为直线x=1.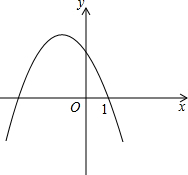 二次函数y=ax2+bx+c的图象如图所示,它与x轴交于点(1,0),则化简二次根式
二次函数y=ax2+bx+c的图象如图所示,它与x轴交于点(1,0),则化简二次根式