题目内容
平面内四条直线最少有a个交点，最多有b个交点，则a+b=（ ）
| A、6 | B、4 | C、2 | D、0 |
考点：直线、射线、线段
专题：计算题
分析：当所有直线两两平行时交点个数最少；交点最多时根据交点个数公式
代入计算即可求解；依此得到a、b的值，再相加即可求解．
| n(n-1) |
| 2 |
解答：解：交点个数最多时，
=
=6，最少有0个．
所以b=6，a=0，
所以 a+b=6．
故选：A．
| n(n-1) |
| 2 |
| 4×3 |
| 2 |
所以b=6，a=0，
所以 a+b=6．
故选：A．
点评：本题考查了相交线的交点问题，熟记公式是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
若⊙01、⊙02的直径分别为8和12，圆心距0102=4，则⊙01与⊙02的位置关系为（ ）
| A、内切 | B、相交 | C、外切 | D、内含 |
-a3•（-a）2的运算结果是（ ）
| A、a5 |
| B、-a5 |
| C、a6 |
| D、-a6 |
已知二次出数y=ax2+bx+c的图象与x轴交于点（-2，0）、（x1，0）且1＜x1＜2，与y轴的正半轴的交点在（0，2）的下方，则①4a-2b+c=0，②a-b＜0，③2a+c＞0，④2a-b+1＜0，其中正确的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
据不完全统计，2012年中国红十字会捐出1049万元人民币的紧急援助．10049万这个数用科学记数法表示为（ ）
| A、1.049×106 |
| B、1.049×107 |
| C、1.049×108 |
| D、1.049×109 |
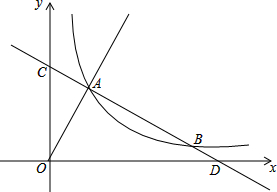已知直线y=-
已知：如图，在△ABC中，DE是中位线，EF∥AB，EF交BC于点F．求证：F是BC的中点．