Question

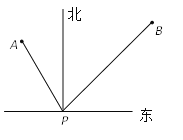
【题目】如图，点P表示某港口的位置，甲船在港口北偏西30°方向距港口50海里的A处，乙船在港口北偏东45°方向距港口60海里的B处，两船同时出发分别沿AP、BP方向匀速驶向港口P，经过1小时，乙船在甲船的正东方向处，已知甲船的速度是海里/时，求乙船的速度．

Answer 1

【答案】（60-20）海里/小时．

【解析】试题分析：根据题意画出图形，求出PC的长，利用三角函数求出PE的长，再根据勾股定理求出DP的长，从而得到BD的长，进而求出船的速度．

试题解析：设一小时后甲船位于C处，乙船位于D处，

∵AC=1×10=10海里，

∴PC=50-10=40海里，

∴PE=40×cos30°=40×海里，

∴PD==20海里，

∴BD=（60-20）海里，

（60-20）÷1=（60-20）海里/小时．