题目内容
如图，∠ACB=∠CDE=90°，B是CE的中点，∠DCE=30°，AC=CD．求证：AB∥DE．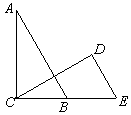 
证明：∵∠CDE=90°，∠DCE=30°
∴
∵B是CE的中点，
∴
∴DE=CB
在△ABC和△CED中
∴△ABC≌△CED
∴∠ABC=∠E
∴AB∥DE.
∴
∵B是CE的中点，
∴
∴DE=CB
在△ABC和△CED中
∴△ABC≌△CED
∴∠ABC=∠E
∴AB∥DE.
首先根据直角三角形30°角所对的直角边等于斜边的一半可得,再有，可得DE=CB，再有条件AC=CD，∠ACB=∠D，可证明△ABC≌△CED，根据全等三角形的性质可得∠ABC=∠E，根据同位角相等，两直线平行可得到结论．
,再有，可得DE=CB，再有条件AC=CD，∠ACB=∠D，可证明△ABC≌△CED，根据全等三角形的性质可得∠ABC=∠E，根据同位角相等，两直线平行可得到结论．
练习册系列答案
相关题目
