题目内容
 (2013•常德)如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=
(2013•常德)如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=| 1 | 3 |
(1)求BC的长;
(2)求tan∠DAE的值.
分析:(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=1;解Rt△ADB,得出AB=3,根据勾股定理求出BD=2
,然后根据BC=BD+DC即可求解;
(2)先由三角形的中线的定义求出CE的值,则DE=CE-CD,然后在Rt△ADE中根据正切函数的定义即可求解.
| 2 |
(2)先由三角形的中线的定义求出CE的值,则DE=CE-CD,然后在Rt△ADE中根据正切函数的定义即可求解.
解答:解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=
,AD=1,
∴AB=
=3,
∴BD=
=2
,
∴BC=BD+DC=2
+1;
(2)∵AE是BC边上的中线,
∴CE=
BC=
+
,
∴DE=CE-CD=
-
,
∴tan∠DAE=
=
-
.
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=
| 1 |
| 3 |
∴AB=
| AD |
| sinB |
∴BD=
| AB2-AD2 |
| 2 |
∴BC=BD+DC=2
| 2 |
(2)∵AE是BC边上的中线,
∴CE=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
∴DE=CE-CD=
| 2 |
| 1 |
| 2 |
∴tan∠DAE=
| DE |
| AD |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的高、中线的定义,勾股定理,解直角三角形,难度中等,分别解Rt△ADC与Rt△ADB,得出DC=1,AB=3是解题的关键.

练习册系列答案
相关题目
 (2013•常德)如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )
(2013•常德)如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( ) (2013•常德)如图,已知⊙O是△ABC的外接圆,若∠BOC=100°,则∠BAC=
(2013•常德)如图,已知⊙O是△ABC的外接圆,若∠BOC=100°,则∠BAC= (2013•常德)如图,已知⊙O是等腰直角三角形ADE的外接圆,∠ADE=90°,延长ED到C使DC=AD,以AD,DC为邻边作正方形ABCD,连接AC,连接BE交AC于点H.求证:
(2013•常德)如图,已知⊙O是等腰直角三角形ADE的外接圆,∠ADE=90°,延长ED到C使DC=AD,以AD,DC为邻边作正方形ABCD,连接AC,连接BE交AC于点H.求证: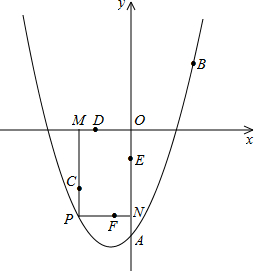 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B(