题目内容
23、已知:如图1,点C为线段AB上一点,△ACM和△CBN都是等边三角形,AN、BM交于点P,由△BCM≌△NCA,易证结论:①BM=AN.


(1)请写出除①外的两个结论:
(2)求出图1中AN和BM相交所得最大角的度数
(3)将△ACM绕C点按顺时针方向旋转180°,使A点落在BC上,请对照原题图形在图2中画出符合要求的图形(不写作法,保留痕迹);
(4)探究图2中AN和BM相交所得的最大角的度数有无变化
(5)在(3)所得到的图形2中,请探究“AN=BM”这一结论是否成立,若成立,请证明;若不成立,请说明理由.


(1)请写出除①外的两个结论:
∠MBC=∠ANC
∠BMC=∠NAC
;(2)求出图1中AN和BM相交所得最大角的度数
120°
;(3)将△ACM绕C点按顺时针方向旋转180°,使A点落在BC上,请对照原题图形在图2中画出符合要求的图形(不写作法,保留痕迹);
(4)探究图2中AN和BM相交所得的最大角的度数有无变化
不变
(填变化或不变);(5)在(3)所得到的图形2中,请探究“AN=BM”这一结论是否成立,若成立,请证明;若不成立,请说明理由.
分析:(1)可根据全等三角形的对应角相等和对应边相等来得出结论;
(2)本题求的是∠APB的度数,∠APB是三角形BNP的外角,因此利用三角形外角的特点得出结论;
(4)要通过证△BMC≌△ACN来实现,根据已知条件来证明这两个三角形两三角形全等,然后根据(2)的步骤即可得出最大角仍是120°;
(5)通过证三角形ANC和BCM全等来得出AN=BM,方法同(4).
(2)本题求的是∠APB的度数,∠APB是三角形BNP的外角,因此利用三角形外角的特点得出结论;
(4)要通过证△BMC≌△ACN来实现,根据已知条件来证明这两个三角形两三角形全等,然后根据(2)的步骤即可得出最大角仍是120°;
(5)通过证三角形ANC和BCM全等来得出AN=BM,方法同(4).
解答:解:(1)∠MBC=∠ANC、∠BMC=∠NAC.
(2)∵∠CNP=∠CBP,
∵∠APB=∠BNC+∠CNP+∠NBP=∠BNC+∠NBP+∠ABP=∠NBC+∠BNC=120°;
(3)

(4)不变;
(5)成立.
证明:∵三角形NBC和AMC都是等边三角形,
∴BC=CN,MC=AC,∠MCB=∠NCA=60°;
∴△CAN≌△MCB;
∴AN=BM.
(2)∵∠CNP=∠CBP,
∵∠APB=∠BNC+∠CNP+∠NBP=∠BNC+∠NBP+∠ABP=∠NBC+∠BNC=120°;
(3)

(4)不变;
(5)成立.
证明:∵三角形NBC和AMC都是等边三角形,
∴BC=CN,MC=AC,∠MCB=∠NCA=60°;
∴△CAN≌△MCB;
∴AN=BM.
点评:本主要考查等边三角形的性质和全等三角形的判定,根据全等三角形来得出相等的边和角是解题的关键.

练习册系列答案
相关题目
 15、已知:如图1,点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN交MC于点E,BM交CN于点F.
15、已知:如图1,点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN交MC于点E,BM交CN于点F.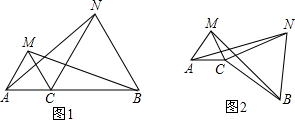 旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明.
旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明.
 (2012•西城区一模)已知:如图,A点坐标为
(2012•西城区一模)已知:如图,A点坐标为