题目内容
(1)已知:如图1,点C为线段AB上一点,△ACM,△CBN是等边三角形,求证:AN=BM,这时可以证明(2)如果去掉“点C为线段AB上一点”的条件,而是让△CBN绕点C
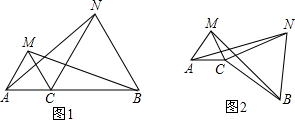 旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明.
旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明.
分析:(1)AN=BM,理由为:由△ACM和△CBN都是等边三角形,根据等边三角形的边长相等分别得到边长相等,三个内角相等,由∠ACM和∠NCB相等,两边加上∠MCN,得到∠ACN与∠MCB相等,利用SAS即可得到三角形ACN与三角形MCB全等,根据全等三角形的对应边相等即可得证;
(2)AN=BM,理由为:由△ACM和△CBN都是等边三角形,根据等边三角形的边长相等分别得到边长相等,三个内角相等,由∠ACM和∠NCB相等,两边加上∠MCN,得到∠ACN与∠MCB相等,利用SAS即可得到三角形ACN与三角形MCB全等,根据全等三角形的对应边相等即可得证.
(2)AN=BM,理由为:由△ACM和△CBN都是等边三角形,根据等边三角形的边长相等分别得到边长相等,三个内角相等,由∠ACM和∠NCB相等,两边加上∠MCN,得到∠ACN与∠MCB相等,利用SAS即可得到三角形ACN与三角形MCB全等,根据全等三角形的对应边相等即可得证.
解答:解:(1)相等.
证明如下:∵△ACM,△CBN是等边三角形,
∴AC=CM,CN=BC,∠ACM=∠BCN=60°,
又∠ACN=∠MCN+∠ACM=∠MCN+60°,∠MCB=∠MCN+∠BCN=∠MCN+60°,
∴∠ACN=∠MCB,
在△ACN和△MCB中
MCB,
∴△ACN≌△MCB(SAS),
∴AN=BM;
(2)相等.
证明如下:∵△ACM,△CBN是等边三角形,
∴AC=CM,CN=BC,∠ACM=∠BCN=60°,
又∠ACN=∠MCN+∠ACM=∠MCN+60°,∠MCB=∠MCN+∠BCN=∠MCN+60°,
在△ACN和△MCB中
MCB,
∴△ACN≌△MCB(SAS),
∴AN=BM.
证明如下:∵△ACM,△CBN是等边三角形,
∴AC=CM,CN=BC,∠ACM=∠BCN=60°,
又∠ACN=∠MCN+∠ACM=∠MCN+60°,∠MCB=∠MCN+∠BCN=∠MCN+60°,
∴∠ACN=∠MCB,
在△ACN和△MCB中
|
∴△ACN≌△MCB(SAS),
∴AN=BM;
(2)相等.
证明如下:∵△ACM,△CBN是等边三角形,
∴AC=CM,CN=BC,∠ACM=∠BCN=60°,
又∠ACN=∠MCN+∠ACM=∠MCN+60°,∠MCB=∠MCN+∠BCN=∠MCN+60°,
在△ACN和△MCB中
|
∴△ACN≌△MCB(SAS),
∴AN=BM.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,证得三角形全等是正确解答本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为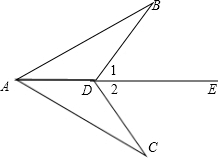 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为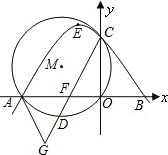 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧