Question

【题目】如图，直线y＝－x＋8与x轴、y轴分别相交于点A、B，设M是OB上一点，若将△ABM沿AM折叠，使点B恰好落在x轴上的点B'处．求：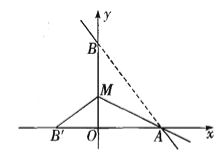

（1）点B'的坐标: ．

（2）直线AM所对应的函数关系式．

Answer 1

【答案】（1）B′的坐标为（－4，0）；（2）y＝－x＋3.

【解析】

试题分析：把x的值代入即可求出y的值，即是点的坐标，再把坐标代入就能求出解析式．

试题解析：解：当x=0时，y=x+8=8，即B（0，8），

当y=0时，x=6，即A（6，0），

所以AB=AB′=10，即B′（-4，0），

因为点B与B′关于AM对称，

所以BB′的中点（-2，4）在直线AM上.

设直线AM的解析式为y=kx+b，把（-2，4），（6，0），

代入可得y=x+3.