题目内容
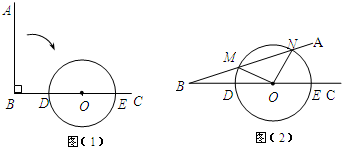
如图(1),∠ABC=90°,O为射线BC上一点,OB=4,以点O为圆心,2
长为半径作⊙O交BC于点D、E.
(1)当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切?请说明理由.
(2)若射线BA绕点B按顺时针方向旋转60°时与⊙O相交于M、N两点,如图(2),求
的长.
| 2 |
(1)当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切?请说明理由.
(2)若射线BA绕点B按顺时针方向旋转60°时与⊙O相交于M、N两点,如图(2),求
 |
| MN |

分析:(1)首先设切点为F,连OF.则OF⊥BF,由特殊角的三角函数值,即可求得∠OBF的度数,继而求得当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切;
(2)首先过点O作OH⊥AB于点H,由射线BA绕点B按顺时针方向旋转60°时与⊙O相交于M、N两点,即可得∠ABC=30°,继而求得OH的长,然后由特殊角的三角函数值,求得∠MOH的度数,继而求得∠MON的度数,然后由弧长公式求得
的长.
(2)首先过点O作OH⊥AB于点H,由射线BA绕点B按顺时针方向旋转60°时与⊙O相交于M、N两点,即可得∠ABC=30°,继而求得OH的长,然后由特殊角的三角函数值,求得∠MOH的度数,继而求得∠MON的度数,然后由弧长公式求得
 |
| MN |
解答: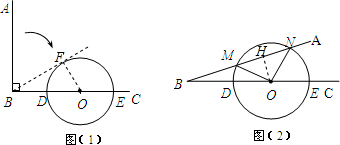 解:(1)当射线BA绕点B按顺时针方向旋转45度°或135°时与⊙O相切.
解:(1)当射线BA绕点B按顺时针方向旋转45度°或135°时与⊙O相切.
理由如下:如图,设切点为F,连OF.则OF⊥BF,
在Rt△OBF中,OF=2
,OB=4,
∴cos∠OBF=
=
,
∴∠OBF=∠BOF=45°,
∴∠ABF=45°,
同理:当∠ABF=135°时,AB旋转的此时BF的反向延长线上,
∴当射线BA绕点B按顺时针方向旋转45度°或135°时与⊙O相切.
(2)过点O作OH⊥AB于点H,
∵射线BA绕点B按顺时针方向旋转60°时与⊙O相交于M、N两点,
∴∠ABC=30°,
∴OH=
OB=
×4=2,
在Rt△OMH中,OM=2
,
∴cos∠MOH=
=
,
∴∠MOH=45°,
∴∠MON=90°,
∴
的长为:
=
π.
 解:(1)当射线BA绕点B按顺时针方向旋转45度°或135°时与⊙O相切.
解:(1)当射线BA绕点B按顺时针方向旋转45度°或135°时与⊙O相切.理由如下:如图,设切点为F,连OF.则OF⊥BF,
在Rt△OBF中,OF=2
| 2 |
∴cos∠OBF=
| BF |
| OB |
| ||
| 2 |
∴∠OBF=∠BOF=45°,
∴∠ABF=45°,
同理:当∠ABF=135°时,AB旋转的此时BF的反向延长线上,
∴当射线BA绕点B按顺时针方向旋转45度°或135°时与⊙O相切.
(2)过点O作OH⊥AB于点H,
∵射线BA绕点B按顺时针方向旋转60°时与⊙O相交于M、N两点,
∴∠ABC=30°,
∴OH=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OMH中,OM=2
| 2 |
∴cos∠MOH=
| OH |
| OM |
| ||
| 2 |
∴∠MOH=45°,
∴∠MON=90°,
∴
 |
| MN |
90×π×2
| ||
| 180 |
| 2 |
点评:此题考查了切线的性质、旋转的性质、直角三角形的性质以及特殊角的三角函数问题.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
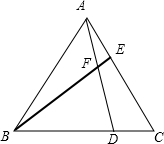 已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD.
已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD. 如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD.
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD. 13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是
13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是 方作等边△CDE,连接BE.
方作等边△CDE,连接BE. 如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的
如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的