题目内容
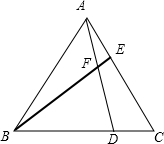 已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD.
已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD.(1)求证:AD=BE;
(2)求:∠BFD的度数.
分析:(1)根据等边三角形各边长相等的性质可得AB=AC,易证△ABE≌△CAD可得AD=BE;
(2)根据全等三角形对应角相等可得∠ABE=∠CAD,进而根据∠BFD=∠BAD+∠ABE即可求∠BFD的度数.
(2)根据全等三角形对应角相等可得∠ABE=∠CAD,进而根据∠BFD=∠BAD+∠ABE即可求∠BFD的度数.
解答:(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠C=60°,AB=CA,
在△ABE和△CAD中
,
∴△ABE≌△CAD(SAS),
∴AD=BE(全等三角形对应边相等);
(2)解:∵△ABE≌△CAD(已证),
∴∠ABE=∠CAD(全等三角形对应角相等),
又∵∠BFD=∠BAD+∠ABE,
∴∠BFD=∠BAD+∠CAD=∠BAC,
又∠BAC=60°,
∴∠BFD=60°.
∴∠BAC=∠C=60°,AB=CA,
在△ABE和△CAD中
|
∴△ABE≌△CAD(SAS),
∴AD=BE(全等三角形对应边相等);
(2)解:∵△ABE≌△CAD(已证),
∴∠ABE=∠CAD(全等三角形对应角相等),
又∵∠BFD=∠BAD+∠ABE,
∴∠BFD=∠BAD+∠CAD=∠BAC,
又∠BAC=60°,
∴∠BFD=60°.
点评:本题考查了全等三角形的证明,全等三角形对应边、对应角相等的性质,等边三角形各内角为60°的性质,本题中求证△ABE≌△CAD是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 类似地你可以得到:“满足
类似地你可以得到:“满足
 ,则等边三角
,则等边三角
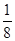 B.
B.  C.
C.
 D.1
D.1