题目内容
已知O是等边△ABC内的一点，∠AOB、∠BOC、∠AOC的角度之比为6：5：4．则在以OA、OB、OC为边的三角形中，此三角形所对的角度之比为______．
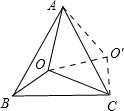
如图，以点A为中心，将△AOB逆时针旋转60°得△AO′C，
则△AO′C≌△AOB，O′C=BO，
又旋转角∠OAO′=60°，AO=AO′，
∴△AOO′为等边三角形，∴OO′=AO，
由已知设∠AOB=6x，∠BOC=5x，∠AOC=4x，则6x+5x+4x=360°，解得x=24°，
∴∠AOB=144°，∠BOC=120°，∠AOC=96°，∠AO′C=∠ABO=144°，
在△OO′C中，由∠OO′C=∠AO′C-∠AO′O=144°-60°=84°，
∠O′OC=∠AOC-∠AOO′=96°-60°=36°，
由内角和定理，得∠OCO′=180°-84°-36°=60°，
∴∠OCO′：∠O′OC：∠OO′C=5：3：7．
故答案为：5：3：7．
则△AO′C≌△AOB，O′C=BO，
又旋转角∠OAO′=60°，AO=AO′，
∴△AOO′为等边三角形，∴OO′=AO，
由已知设∠AOB=6x，∠BOC=5x，∠AOC=4x，则6x+5x+4x=360°，解得x=24°，
∴∠AOB=144°，∠BOC=120°，∠AOC=96°，∠AO′C=∠ABO=144°，
在△OO′C中，由∠OO′C=∠AO′C-∠AO′O=144°-60°=84°，
∠O′OC=∠AOC-∠AOO′=96°-60°=36°，
由内角和定理，得∠OCO′=180°-84°-36°=60°，
∴∠OCO′：∠O′OC：∠OO′C=5：3：7．
故答案为：5：3：7．
练习册系列答案
相关题目
、BF相交于M，DC、AB相交于N．
