题目内容
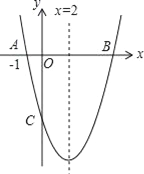
【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)
【答案】(1)y=x2﹣4x﹣5;(2)B(5,0),C(0,﹣5);(3)![]() π.
π.
【解析】试题分析:(1)利用对称轴方程可求得b,把点A的坐标代入可求得c,可求得抛物线的解析式;(2)根据A、B关于对称轴对称可求得点B的坐标,利用抛物线的解析式可求得B点坐标;(3)根据B、C坐标可求得BC长度,由条件可知BC为过O、B、C三点的圆的直径,可求得圆的面积.
试题解析:(1)由A(﹣1,0),对称轴为x=2,可得 ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2﹣4x﹣5;
(2)由A点坐标为(﹣1,0),且对称轴方程为x=2,可知AB=6,
∴OB=5,
∴B点坐标为(5,0),
∵y=x2﹣4x﹣5,
∴C点坐标为(0,﹣5);
(3)如图,连接BC,则△OBC是直角三角形,

∴过O、B、C三点的圆的直径是线段BC的长度,
在Rt△OBC中,OB=OC=5,
∴BC=5![]() ,
,
∴圆的半径为![]() ,
,
∴圆的面积为π(![]() )2=
)2=![]() π.
π.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目


