题目内容
【题目】如图:在等边三角形ABC中,点E在线段AB上,点D在CB的延长线上,![]()
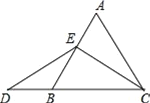
(1)试证明△DEC是等腰三角形;(2)在图中找出与AE相等的线段,并证明
【答案】(1)证明见解析;(2)BD=AE,证明见解析.
【解析】
(1)根据等边三角形的性质可得∠ABC=∠ACB,由三角形外角的性质可得∠ABC=∠D+∠DEB,再根据∠ACB=∠ACE+∠ECB,∠ACE=∠DEB,推得∠D=∠ECB即可得到结论;
(2)图中BD=AE,证明过程为:在AC上截取AF=AE,则可得△AEF是等边三角形,通过推导得出BE=CF,AE=EF,∠EFC=∠DBE,然后利用ASA证明△DEB≌△ECF,根据全等三角形的性质以及等量代换即可得.
(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵∠ABC是△DBE的外角,
∴∠ABC=∠D+∠DEB,
∵∠ACB=∠ACE+∠ECB,∠ACE=∠DEB,
∴∠D=∠ECB,
∴ED=EC,
即△DEC是等腰三角形;
(2)BD=AE,证明如下:
如图,在AC上截取AF=AE,
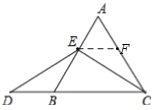
∵△ABC是等边三角形,
∴∠A=∠ABC=60°,AB=AC,
∴∠EBD=120°,AB-AE=AC-AF,△AEF是等边三角形,
∴BE=CF,AE=EF,∠AFE=60°,
∴∠EFC=120°,
∴∠EFC=∠DBE,
在△DBE和△EFC中,
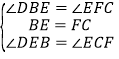 ,
,
∴△DEB≌△ECF,
∴BD=EF,
∴BD=AE.

 口算题天天练系列答案
口算题天天练系列答案【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?