Question

【题目】如图，在矩形ABCD中，AB=5，BC=7，点E是AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A′恰好落在∠BCD的平分线上时，CA′的长为（ ）
A.3或4
B.3 或4
C.3或4
D.4或3

Answer 1

【答案】B
【解析】解：如图，过点A1作A1M⊥BC于点M．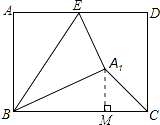
∵点A的对应点A1恰落在∠BCD的平分线上，
∴设CM=A1M=x，则BM=7﹣x．
又由折叠的性质知AB=A1B=5．
∴在直角△A1MB中，由勾股定理得到：A1M2=A1B2﹣BM2=25﹣（7﹣x）2 ．
∴25﹣（7﹣x）2=x2 ，
解得：x1=3，x2=4，
∵在等腰Rt△A1CM中，CA1= A1M．
∴CA1=3 或4 ．
故选：B．
如图，过点A1作A1M⊥BC于点M．设CM=A1M=x，则BM=4﹣x．在直角△A1MB中，由勾股定理得到：A1M2=A1B2﹣BM2=25﹣（7﹣x）2 ． 由此求得x的值；然后在等腰Rt△A1CM中，得到CA1= A1M．