题目内容
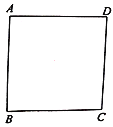
【题目】如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（ ）
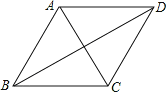
A. △ABD与△ABC的周长相等
B. △ABD与△ABC的面积相等
C. 菱形的周长等于两条对角线之和的两倍
D. 菱形的面积等于两条对角线之积的两倍
【答案】B
【解析】试题分析：分别利用菱形的性质结合各选项进而求出即可．
试题解析：A、∵四边形ABCD是菱形，
∴AB=BC=AD，
∵AC＜BD，
∴△ABD与△ABC的周长不相等，故此选项错误；
B、∵S△ABD=
S平行四边形ABCD，S△ABC=S平行四边形ABCD，
∴△ABD与△ABC的面积相等，故此选项正确；
C、菱形的周长与两条对角线之和不存在固定的数量关系，故此选项错误；
D、菱形的面积等于两条对角线之积的，故此选项错误；
故选B．
智能训练练测考系列答案
计算高手系列答案【题目】我市某中学举行“中国梦校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．
（1）根据图示填写下表；
平均数（分） | 中位数（分） | 众数（分） | |
初中部 | 85 | ||
高中部 | 85 | 100 |
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
【题目】某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．
（1）求该种水果每次降价的百分率；
（2）从第一次降价的第1天算起，第x天（x为整数）的售价、销量及储存和损耗费用的相关信息如表所示．已知该种水果的进价为4.1元/斤，设销售该水果第x（天）的利润为y（元），求y与x（1≤x＜15）之间的函数关系式，并求出第几天时销售利润最大？
时间x（天） | 1≤x＜9 | 9≤x＜15 | x≥15 |
售价（元/斤） | 第1次降价后的价格 | 第2次降价后的价格 | |
销量（斤） | 80﹣3x | 120﹣x | |
储存和损耗费用（元） | 40+3x | 3x2﹣64x+400 | |
（3）在（2）的条件下，若要使第15天的利润比（2）中最大利润最多少127.5元，则第15天在第14天的价格基础上最多可降多少元？
