题目内容
如图, 等腰梯形两底之差等于一腰的长，那么这个梯形较小内角的度数是
A． | B． | C． | D． |
B
分析：过点D作DE∥AB，交BC于点E，根据已知及等腰梯形的性质得到△DEC是等边三角形，从而得到梯形的一内角为60°．
解答：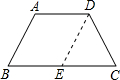
解：如图，过点D作DE∥AB，交BC于点E．
由已知知等腰梯形两底之差等于一腰的长，
故可得DC=DE，又知AB=DE，
即△DEC是等边三角形，所以∠C=60°，
故这个梯形较小内角的度数是60°，
故选B．
解答：
解：如图，过点D作DE∥AB，交BC于点E．由已知知等腰梯形两底之差等于一腰的长，
故可得DC=DE，又知AB=DE，
即△DEC是等边三角形，所以∠C=60°，
故这个梯形较小内角的度数是60°，
故选B．
练习册系列答案
相关题目
C于点E，过点E作DH的垂线交线段AB、CD于点F、G．
明理由．
、
分别是平行四边形
的边
、
上的点，
与
相交于点
，
与
相交于点
，若
△APD 
，
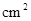