题目内容
【题目】某市为推进养老服务工作的深入开展,在扩大社区养老覆盖率、规范机构养老、科学规划养老服务布局等方面作了大量工作.该市的养老机构拥有的养老床位数从2016年底的2万个增长到2018年底的2.88万个:
(1)求该市这两年养老床位数的年平均增长率:
(2)该市2018年底正在筹建一社区养老中心,按照规划拟建造三类养老专用房间(一个养老床位的单人间、两个养老床位的双人间、三个养老床位的三人间)共100间,若按规划需要建造的单人间的房间数为![]() (
(![]() ),双人间的房间数是单人间的2倍,求该养老中心建成后最多可提供养老床位多少个?最少提供养老床位多少个?
),双人间的房间数是单人间的2倍,求该养老中心建成后最多可提供养老床位多少个?最少提供养老床位多少个?
【答案】(1)该市这两年拥有的养老床位数的平均年增长率为20;(2)该养老中心建成后最多提供养老床位252个,最少提供养老床位240个.
【解析】
(1)设该市这两年(从2016年度到2018年底)拥有的养老床位数的平均年增长率为x,根据“2018年的床位数=2016年的床位数×(1+增长率)2”,列出关于x的一元二次方程,解方程即可得出结论;(2)由题意可知规划建造单人间的房间数为![]()
![]() ,则建造双人间的房间数为
,则建造双人间的房间数为![]() ,三人间的房间数为
,三人间的房间数为![]() ,设该养老中心建成后能提供养老床位y个,根据“可提供的床位数=单人间数+2倍的双人间数+3倍的三人间数”即可得出y关于m的函数关系式,根据一次函数的性质结合m的取值范围,即可得出结论.
,设该养老中心建成后能提供养老床位y个,根据“可提供的床位数=单人间数+2倍的双人间数+3倍的三人间数”即可得出y关于m的函数关系式,根据一次函数的性质结合m的取值范围,即可得出结论.
(1)设该市这两年拥有的养老床位数的平均年增长率为,由题意可列出方程:
![]() ,
,
解得![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
答:该市这两年拥有的养老床位数的平均年增长率为20%.
(2)设规划建造单人间的房间数为![]()
![]() ,则建造双人间的房间数为
,则建造双人间的房间数为![]() ,
,
三人间的房间数为![]() ,
,
设该养老中心建成后能提供养老床位![]() 个,
个,
由题意得:![]()
∵![]() 随
随![]() 的增大而减小
的增大而减小
∴当![]() 时,
时,![]() 的最大值为252.
的最大值为252.
当![]() 时,
时,![]() 的最小值为240.
的最小值为240.
答:该养老中心建成后最多提供养老床位252个,最少提供养老床位240个.

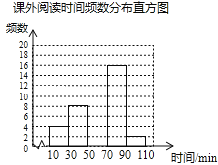
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?