Question

【题目】如图，P、Q是△ABC边上的两点，且BP=PQ=QC=AP=AQ，求∠BAC的度数.

Answer 1

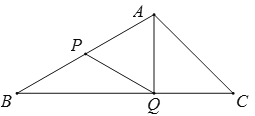
【答案】∠BAC=105°.

【解析】

由BP=PQ=QC=AP=AQ，可得∠PAQ=∠APQ=∠AQP=60°，∠B=∠BQP，∠C=∠CAQ，继而根据三角形外角的性质可得∠BQP=30°，继而可得∠AQB=90°，从而求得∠CAQ=45°，再由∠BAC=∠BAQ+∠CAQ即可求得答案.

∵BP=PQ=QC=AP=AQ，

∴∠PAQ=∠APQ=∠AQP=60°，∠B=∠BQP，∠C=∠CAQ，

又∵∠BQP+∠ABQ=∠APQ，∠C+∠CAQ=∠AQB，

∴∠BQP=30°，

∴∠AQB=∠BQP+∠AQP=90°，

∴∠CAQ=45°，

∴∠BAC=∠BAQ+∠CAQ=105°.