Question

【题目】某菜农搭建了一个横截面为抛物线的大棚，尺寸如图：

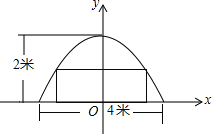
（1）如图建立平面直角坐标系，使抛物线对称轴为y轴，求该抛物线的解析式；

（2）若需要开一个截面为矩形的门（如图所示），已知门的高度为1.60米，那么门的宽度最大是多少米（不考虑材料厚度）？（结果保留根号）

Answer 1

【答案】（1）y=﹣x2+2；（2）米．

【解析】

试题分析：（1）根据题意设出二次函数的解析式，把图象上点的坐标代入即可求出二次函数的解析式；

（2）令y=1.6，求出x的值，即可确定门的最大宽度．

解：（1）由图可设抛物线的解析式为：y=ax2+2，

由图知抛物线与x轴正半轴的交点为（2，0），则：a×22+2=0，

∴a=﹣，

∴抛物线的解析式为y=﹣x2+2；

（2）当y=1.60时，知1.6=﹣x2+2，

解得：x=，

所以门的宽度最大为2×=米．