Question

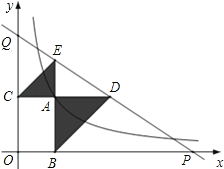
【题目】如图，已知动点A在函数的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC．直线DE分别交x，y轴分别于点P，Q．当QE：DP=4：9时，图中阴影部分的面积等于 ．

Answer 1

【答案】

【解析】

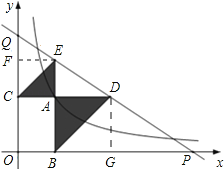
试题分析：过点D作DG⊥x轴于点G，过点E作EF⊥y轴于点F．令A（t，），则AD=AB=DG=，AE=AC=EF=t，则图中阴影部分的面积=△ACE的面积+△ABD的面积=t2+×，因此只需求出t2的值即可．先在直角△ADE中，由勾股定理，得出DE=，再由△EFQ∽△DAE，求出QE=，△ADE∽△GPD，求出DP=：，然后根据QE：DP=4：9，即可得出t2=．

解：解法一：过点D作DG⊥x轴于点G，过点E作EF⊥y轴于点F．

令A（t，），则AD=AB=DG=，AE=AC=EF=t．

在直角△ADE中，由勾股定理，得DE====．

∵△EFQ∽△DAE，

∴QE：DE=EF：AD，

∴QE=，

∵△ADE∽△GPD，

∴DE：PD=AE：DG，

∴DP=．

又∵QE：DP=4：9，

∴：=4：9，

解得t2=．

∴图中阴影部分的面积=AC2+AB2=t2+×=+3=；

解法二：∵QE：DP=4：9，

∴EF：PG=4：9，

设EF=4t，则PG=9t，

∴A（4t，），

由AC=AE AD=AB，

∴AE=4t，AD=，DG=，GP=9t，

∵△ADE∽△GPD，

∴AE：DG=AD：GP，

4t：=：9t，即t2=，

图中阴影部分的面积=4t×4t+××=．

故答案为：．