题目内容
【题目】如图,某河堤的横断面是梯形ABCD,BC∥AD,BE⊥AD于点E,AB=50米,BC=30米,∠A=60°,∠D=30°.求AD的长度.
【答案】解:作CF⊥AD于点F, 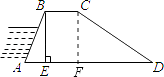
∵BE⊥AD,AB=50米,∠A=60°,
∴BE=ABsin60°=50× ![]() =25
=25 ![]() ,
,
∴AE= ![]() =25,
=25,
∵BC∥AD,CF⊥AD,
∴CF=BE=25,EF=BC=30,在Rt△CFD中,∠D=30°,
∴FD= ![]()
= ![]() =75,
=75,
∴AD=AE+EF+FD=25+30+75=130(米).
【解析】作CF⊥AD于点F,在Rt△ABE中,利用锐角三角形函数得出BE的长,再利用勾股定理得出AE的长,根据题意知四边形EFCB是矩形,根据矩形的性质得出CF=BE=25,EF=BC=30,在Rt△CFD中,∠D=30°,根据正切函数的定义得出FD的长,然后根据AD=AE+EF+FD得出答案。

练习册系列答案
相关题目