题目内容
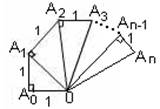
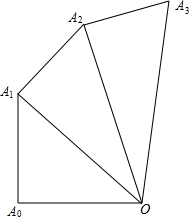 图中的螺旋形由一系列直角三角形组成:△OA0A1是直角边为1的直角三角形,以△OA0A1的斜边OA1为直角边,1为另一直角边,画第二个直角三角形…,依此类推
图中的螺旋形由一系列直角三角形组成:△OA0A1是直角边为1的直角三角形,以△OA0A1的斜边OA1为直角边,1为另一直角边,画第二个直角三角形…,依此类推
(1)求OA3;
(2)写出第n个三角形的面积Sn;
(3)求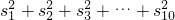 的值.
的值.
解:(1)由勾股定理得:OA1= =
= ,
,
OA2=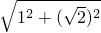 =
= ,
,
OA3= =
= =2;
=2;
(2)由(1)得:第n个直角三角形的直角边是1和 ,
,
则第n个三角形的面积Sn= ×1×
×1× =
=
 ;
;
(3)S1= ×1×1=
×1×1= ,S2=
,S2= ×1×
×1× =
=
 ,S3=
,S3= ×1×
×1× =
=
 ,
,
∴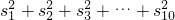 的值
的值
=( )2+(
)2+(
 )2+(
)2+(
 )2+…+(
)2+…+(
 )2
)2
= ×(1+2+3+4+5+6+7+8+9+10)
×(1+2+3+4+5+6+7+8+9+10)
= .
.
分析:(1)根据勾股定理求出各个斜边长即可;
(2)根据勾股定理求出各个斜边长即可;
(3)分别求出各个直角三角形的面积,再代入求出即可.
点评:本题考查了勾股定理的应用,注意:在一个直角三角形中,两直角边的平方和等于斜边的平方,解此题的关键是求出各个斜边的长.
 =
= ,
,OA2=
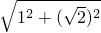 =
= ,
,OA3=
 =
= =2;
=2;(2)由(1)得:第n个直角三角形的直角边是1和
 ,
,则第n个三角形的面积Sn=
 ×1×
×1× =
=
 ;
;(3)S1=
 ×1×1=
×1×1= ,S2=
,S2= ×1×
×1× =
=
 ,S3=
,S3= ×1×
×1× =
=
 ,
,∴
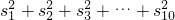 的值
的值=(
 )2+(
)2+(
 )2+(
)2+(
 )2+…+(
)2+…+(
 )2
)2=
 ×(1+2+3+4+5+6+7+8+9+10)
×(1+2+3+4+5+6+7+8+9+10)=
 .
.分析:(1)根据勾股定理求出各个斜边长即可;
(2)根据勾股定理求出各个斜边长即可;
(3)分别求出各个直角三角形的面积,再代入求出即可.
点评:本题考查了勾股定理的应用,注意:在一个直角三角形中,两直角边的平方和等于斜边的平方,解此题的关键是求出各个斜边的长.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
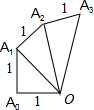 图中的螺旋形由一系列直角三角形组成,则以第n个三角形的斜边长为边长的正方形的面积为
图中的螺旋形由一系列直角三角形组成,则以第n个三角形的斜边长为边长的正方形的面积为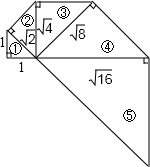 图中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤…,则第n个等腰直角三角形的斜边长为
图中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤…,则第n个等腰直角三角形的斜边长为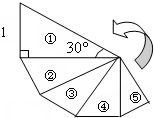 如图中的螺旋形由一系列含30°的直角三角形组成,其序号依次为①、②、③、④、⑤…,则第7个直角三角形的斜边长为
如图中的螺旋形由一系列含30°的直角三角形组成,其序号依次为①、②、③、④、⑤…,则第7个直角三角形的斜边长为 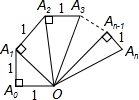 如图,图中的螺旋形由一系列直角三角形组成,则第n个直角三角形的面积为:
如图,图中的螺旋形由一系列直角三角形组成,则第n个直角三角形的面积为: