Question

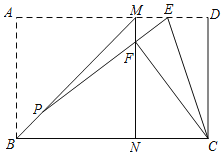
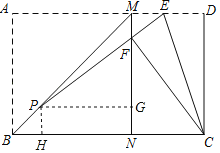
【题目】如图，在矩形纸片ABCD中，将AB沿BM翻折，使点A落在BC上的点N处，BM为折痕，连接MN；再将CD沿CE翻折，使点D恰好落在MN上的点F处，CE为折痕，连接EF并延长交BM于点P，若AD＝8，AB＝5，则线段PE的长等于_____．

Answer 1

【答案】

【解析】

根据折叠可得ABNM是正方形，CD＝CF＝5，∠D＝∠CFE＝90，ED＝EF，可求出三角形FNC的三边为3，4，5，在Rt△MEF中，由勾股定理可以求出三边的长，通过作辅助线，可证△FNC∽△PGF，三边占比为3：4：5，设未知数，通过PG＝HN，列方程求出待定系数，进而求出PF的长，然后求PE的长．

过点P作PG⊥FN，PH⊥BN，垂足为G、H，

由折叠得：ABNM是正方形，AB＝BN＝NM＝MA＝5，

CD＝CF＝5，∠D＝∠CFE＝90，ED＝EF，

∴NC＝MD＝8﹣5＝3，

在Rt△FNC中，FN＝＝4，

∴MF＝5﹣4＝1，

在Rt△MEF中，设EF＝x，则ME＝3﹣x，由勾股定理得，

12+（3﹣x）2＝x2，

解得：x＝，

∵∠CFN+∠PFG＝90，∠PFG+∠FPG＝90，

∴∠CFN=∠PFG

∴△FNC∽△PGF，

∴FG：PG：PF＝NC：FN：FC＝3：4：5，

设FG＝3m，则PG＝4m，PF＝5m，

∴GN＝PH＝BH＝4﹣3m，HN＝5﹣（4﹣3m）＝1+3m＝PG＝4m，

解得：m＝1，

∴PF＝5m＝5，

∴PE＝PF+FE＝5+＝，

故答案为：．