题目内容
【题目】已知:如图1,图2,在平面直角坐标系xOy中,A(0,4),B(0,2),点C在x轴的正半轴上,点D为OC的中点.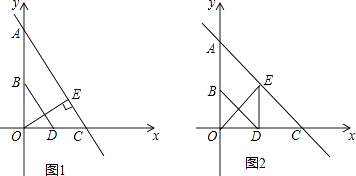
(1)求证:BD∥AC;
(2)如果OE⊥AC于点E,OE=2时,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
【答案】
(1)
证明:∵A(0,4),B(0,2),
∴OA=4,OB=2,点B为线段OA的中点,
∵点D为OC的中点.
∴BD∥AC.
(2)
解:∵OE⊥AC于点E,
∴△AOE是直角三角形.
∵OA=4,OE=2= ![]() OA,
OA,
∴∠OAE=30°.
∵∠AOC=90°,∠OAC=30°,
∴AC=2OC.
在Rt△AOC中,由勾股定理可得:OC2+OA2=AC2,
即OC2+16=4OC2,解得:OC= ![]() ,
,
∵点C在x轴的正半轴上,
∴点C的坐标为( ![]() ,0)
,0)
(3)
解:连接BE,如图所示.
当四边形ABDE为平行四边形时,DE∥AB,DE=AB.
由(1)知点B为线段OA的中点,
∴DE∥OB,DE=OB,
∴四边形ODEB是平行四边形,
∵OB⊥OC,
∴ODEB是矩形.
∵BD∥AC,OE⊥AC,
∴OE⊥BD,
∴矩形ODEB是正方形,
∴OD=OB=2.
∵点D为OC的中点,
∴OC=2OD=4,
∵点C在x轴的正半轴上,
∴点C的坐标为(4,0).
设直线AC的解析式为y=kx+b(k≠0),
把点A(0,4)、C(4,0)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴直线AC的解析式为y=﹣x+4.
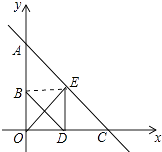
【解析】(1)由点A、B的坐标可得出点B为线段OA的中点,再结合点D为线段OC的中点,即可证得BD∥AC;(2)在Rt△AOE中,由OA、OE的长即可得出∠OAE的度数,在Rt△AOC中可得出AC、OC的关系,再利用勾股定理即可得出OC的长度,根据点C的位置即可得出点C的坐标;(3)连接BE,根据正方形的判定即可得出四边形ODEB是正方形,由正方形的性质即可得出点D的坐标,进而得出点C的坐标,再根据点A、C的坐标利用待定系数法即可求出直线AC的解析式.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案