ЬтФПФкШн
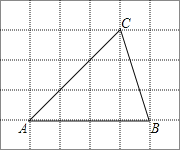
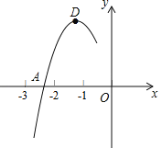
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуAЃЈ2ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ![]() ЃЉЃЌЕуOЃЈ0ЃЌ0ЃЉЃЎЁїAOBШЦзХOЫГЪБеыа§зЊЃЌЕУЁїA'OB'ЃЌЕуAЁЂBа§зЊКѓЕФЖдгІЕуЮЊA'ЃЌB'ЃЌМЧа§зЊНЧЮЊІСЃЎ
ЃЉЃЌЕуOЃЈ0ЃЌ0ЃЉЃЎЁїAOBШЦзХOЫГЪБеыа§зЊЃЌЕУЁїA'OB'ЃЌЕуAЁЂBа§зЊКѓЕФЖдгІЕуЮЊA'ЃЌB'ЃЌМЧа§зЊНЧЮЊІСЃЎ
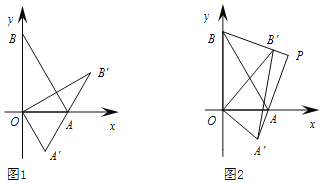
ЃЈЂёЃЉШчЭМ1ЃЌA'B'ЧЁКУОЙ§ЕуAЪБЃЌЧѓДЫЪБа§зЊНЧІСЕФЖШЪ§ЃЌВЂЧѓГіЕуB'ЕФзјБъЃЛ
ЃЈЂђЃЉШчЭМ2ЃЌШє0ЁуЃМІСЃМ90ЁуЃЌЩшжБЯпAA'КЭжБЯпBB'НЛгкЕуPЃЌЧѓжЄЃКAA'ЁЭBB'ЃЛ
ЃЈЂѓЃЉШє0ЁуЃМІСЃМ360ЁуЃЌЧѓЃЈЂђЃЉжаЕФЕуPзнзјБъЕФзюаЁжЕЃЈжБНгаДГіНсЙћМДПЩЃЉЃЎ
ЁОД№АИЁПЃЈЂёЃЉІСЃН60ЁуЃЌB'ЃЈ3ЃЌ![]() ЃЉЃЛЃЈЂђЃЉМћНтЮіЃЛЃЈЂѓЃЉЕуPзнзјБъЕФзюаЁжЕЮЊ
ЃЉЃЛЃЈЂђЃЉМћНтЮіЃЛЃЈЂѓЃЉЕуPзнзјБъЕФзюаЁжЕЮЊ![]() Љ2ЃЎ
Љ2ЃЎ
ЁОНтЮіЁП
ЃЈЂёЃЉзїИЈжњЯп,ЯШИљОнЕуAЃЈ2,0ЃЉ,ЕуBЃЈ0,![]() ЃЉ,ШЗЖЈЁЯABOЃН30Ёу,жЄУїЁїAOA'ЪЧЕШБпШ§НЧаЮ,ЕУа§зЊНЧІСЃН60Ёу,жЄУїЁїCOB'ЪЧ30ЁуЕФжБНЧШ§НЧаЮ,ПЩЕУB'ЕФзјБъ;
ЃЉ,ШЗЖЈЁЯABOЃН30Ёу,жЄУїЁїAOA'ЪЧЕШБпШ§НЧаЮ,ЕУа§зЊНЧІСЃН60Ёу,жЄУїЁїCOB'ЪЧ30ЁуЕФжБНЧШ§НЧаЮ,ПЩЕУB'ЕФзјБъ;
ЃЈЂђЃЉвРОна§зЊЕФаджЪПЩЕУЁЯBOB'ЃНЁЯAOA'ЃНІС,OBЃНOB',OAЃНOA',МДПЩЕУГіЁЯOBB'ЃНЁЯOA'AЃН![]() ЃЈ180ЁуЉІСЃЉ,дйИљОнЁЯBOA'ЃН90Ёу+ІС,ЫФБпаЮOBPA'ЕФФкНЧКЭЮЊ360Ёу,МДПЩЕУЕНЁЯBPA'ЃН90Ёу,МДAA'ЁЭBB';
ЃЈ180ЁуЉІСЃЉ,дйИљОнЁЯBOA'ЃН90Ёу+ІС,ЫФБпаЮOBPA'ЕФФкНЧКЭЮЊ360Ёу,МДПЩЕУЕНЁЯBPA'ЃН90Ёу,МДAA'ЁЭBB';
ЃЈЂѓЃЉзїABЕФжаЕуMЃЈ1,![]() ЃЉ,СЌНгMP,вРОнЕуPЕФЙьМЃЮЊвдЕуMЮЊдВаФ,вдMPЃН
ЃЉ,СЌНгMP,вРОнЕуPЕФЙьМЃЮЊвдЕуMЮЊдВаФ,вдMPЃН![]() ABЃН2ЮЊАыОЖЕФдВ,МДПЩЕУЕНЕБPMЁЮyжсЪБ,ЕуPзнзјБъЕФзюаЁжЕЮЊ
ABЃН2ЮЊАыОЖЕФдВ,МДПЩЕУЕНЕБPMЁЮyжсЪБ,ЕуPзнзјБъЕФзюаЁжЕЮЊ![]() Љ2.
Љ2.
НтЃКЃЈЂёЃЉШчЭМ1ЃЌЙ§B'зїB'CЁЭxжсгкC,
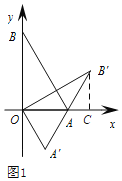
ЁпOAЃН2,OBЃН2![]() ,ЁЯAOBЃН90Ёу,
,ЁЯAOBЃН90Ёу,
ЁрЁЯABOЃН30Ёу,ЁЯBAOЃН60Ёу,
гЩа§зЊЕУЃКOAЃНOA',ЁЯA'ЃНЁЯBAOЃН60Ёу,
ЁрЁїOAA'ЪЧЕШБпШ§НЧаЮ,
ЁрІСЃНЁЯAOA'ЃН60Ёу,
ЁпOBЃНOB'ЃН2![]() ,ЁЯCOB'ЃН90ЁуЉ60ЁуЃН30Ёу,
,ЁЯCOB'ЃН90ЁуЉ60ЁуЃН30Ёу,
ЁрB'CЃН![]() OBЁЏЃН
OBЁЏЃН![]() ,
,
ЁрOCЃН3,
ЁрB'ЃЈ3,![]() ЃЉ,
ЃЉ,
ЃЈЂђЃЉжЄУїЃКШчЭМ2,ЁпЁЯBOB'ЃНЁЯAOA'ЃНІС,OBЃНOB',OAЃНOA',
ЁрЁЯOBB'ЃНЁЯOA'AЃН![]() ЃЈ180ЁуЉІСЃЉ,
ЃЈ180ЁуЉІСЃЉ,
ЁпЁЯBOA'ЃН90Ёу+ІС,ЫФБпаЮOBPA'ЕФФкНЧКЭЮЊ360Ёу,
ЁрЁЯBPA'ЃН360ЁуЉЃЈ180ЁуЉІСЃЉЉЃЈ90Ёу+ІСЃЉЃН90Ёу,
МДAA'ЁЭBB';
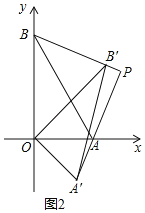
ЃЈЂѓЃЉЕуPзнзјБъЕФзюаЁжЕЮЊ![]() -2ЃЎРэгЩЪЧЃК
-2ЃЎРэгЩЪЧЃК
ШчЭМЃЌзїABЕФжаЕуMЃЈ1,![]() ЃЉ,СЌНгMP,
ЃЉ,СЌНгMP,

ЁпЁЯAPBЃН90Ёу,
ЁрЕуPЕФЙьМЃЮЊвдЕуMЮЊдВаФ,вдMPЃН![]() ABЃН2ЮЊАыОЖЕФдВ,Г§ШЅЕуЃЈ2,2
ABЃН2ЮЊАыОЖЕФдВ,Г§ШЅЕуЃЈ2,2![]() ЃЉ,
ЃЉ,
ЁрЕБPMЁЭxжсЪБ,ЕуPзнзјБъЕФзюаЁжЕЮЊ![]() Љ2ЃЎ
Љ2ЃЎ

 ЬсЗжАйЗжАйМьВтОэЯЕСаД№АИ
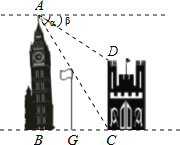
ЬсЗжАйЗжАйМьВтОэЯЕСаД№АИЁОЬтФПЁПШ№АВЪаВмДхеђЁААЫАйФъЕЦЛсЁБГЩЮЊЮТжнЁАЩъвХЁБЕФБІЙѓЯюФПЃЎФГЙЋЫОЩњВњСЫвЛжжМЭФюЛЈЕЦЃЌУПМўМЭФюЛЈЕЦжЦдьГЩБОЮЊ18дЊЃЎЩшЯњЪлЕЅМлxЃЈдЊЃЉЃЌУПШеЯњЪлСПyЃЈМўЃЉУПШеЕФРћШѓwЃЈдЊЃЉЃЎдкЪдЯњЙ§ГЬжаЃЌУПШеЯњЪлСПyЃЈМўЃЉЁЂУПШеЕФРћШѓwЃЈдЊЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфДцдквЛЖЈЕФЙиЯЕЃЌЦфМИзщЖдгІСПШчЯТБэЫљЪОЃК
ЃЈдЊЃЉ | 19 | 20 | 21 | 30 |
ЃЈМўЃЉ | 62 | 60 | 58 | 40 |
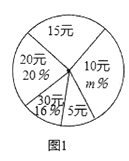
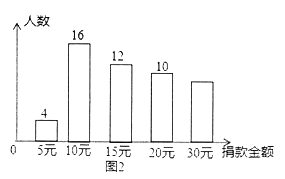
ЃЈ1ЃЉИљОнБэжаЪ§ОнЕФЙцТЩЃЌЗжБ№аДГіАШеЯњЪлСПyЃЈМўЃЉЃЌУПШеЕФРћШѓwЃЈдЊЃЉЙигкЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§БэДяЪНЃЎЃЈРћШѓЃНЃЈЯњЪлЕЅМлЉГЩБОЕЅМлЃЉЁСЯњЪлМўЪ§ЃЉЃЎ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌЙЋЫОУПШеФмЙЛЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉИљОнЮяМлОжЙцЖЈЃЌетжжМЭФюЦЗЕФЯњЪлЕЅМлВЛЕУИпгк32дЊЃЌШчЙћЙЋЫОвЊЛёЕУУПШеВЛЕЭгк350дЊЕФРћШѓЃЌФЧУДжЦдьетжжМЭФюЛЈЕЦУПШеЕФзюЕЭжЦдьГЩБОашвЊЖрЩйдЊЃП