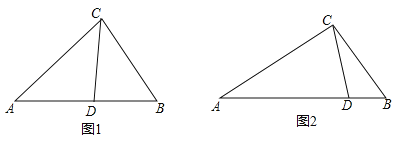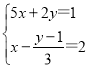题目内容
【题目】如图1,点I是△ABC的内心,AI的延长线交△ABC的外接圆⊙O于点D.

(1)求证:DB=DC=DI;
(2)若AB是⊙O的直径,OI⊥AD,求tan![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)要证明ID=BD=DC,只要求得∠BID=∠IBD,再根据角平分线的性质即可得到结论;
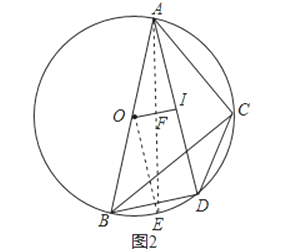
(2)由AB是⊙O的直径,得到BD⊥AD,由于OI⊥AD,得到OI∥BD,于是求得AD=2BD,BD=2OI,设OI=x,则BD=AI=2x,AD=4x,得到AB= ![]() ,如图2,过O作OE⊥BD交⊙O于E,连接AE交OI于F,则OE∥AI,得到比例式代入求得IF=
,如图2,过O作OE⊥BD交⊙O于E,连接AE交OI于F,则OE∥AI,得到比例式代入求得IF= ![]() ,即可得到结果.
,即可得到结果.
试题解析:(1)证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BID=∠ABI+∠BAD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD,
∵∠BAD=∠CAD,
∴![]() ,
,
∴CD=BD,
∴DB=DC=DI;
(2)∵AB是⊙O的直径,
∴BD⊥AD,OI⊥AD,
∴OI∥BD,
∵OA=OB,
∴AI=DI,
由(1)知ID=BD,
∴AD=2BD,BD=2OI,
设OI=x,则BD=AI=2x,AD=4x,
∴AB= ![]() ,
,
如图2,过O作OE⊥BD交⊙O于E,连接AE交OI于F,则OE∥AI,
∴![]() ,
,
即![]() ,
,
∴IF= ![]() ,
,
∵OE⊥BD,
∴![]() ,
,
∴∠DAE=![]() ∠BAD=
∠BAD=![]() ∠CAD,
∠CAD,
∴tan∠DAE= tan![]() =
=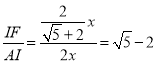 .
.

练习册系列答案
相关题目