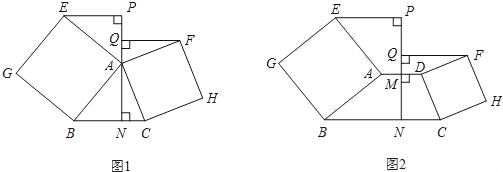
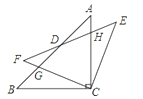
��Ŀ����
����Ŀ����֪�����κ���y=-![]() x2+bx+c(a��0)��ͼ����x�ύ�ڵ�A(-3��0)��B��1��0��������ΪC.
x2+bx+c(a��0)��ͼ����x�ύ�ڵ�A(-3��0)��B��1��0��������ΪC.
(1)��ö��κ����Ľ���ʽ�Ͷ���C�����ꣻ
(2)��ͼ����B��C������ֱ�ߣ������߶�BC�ظ�ֱ������ƽ�ƣ���B��C�ֱ�ƽ�Ƶ���D��E��������F��������κ�����ͼ���ϣ��ҡ�DEF����EFΪб�ߵĵ���ֱ�������Σ����F�����ꣻ
(3)��ȷ��ʵ��p��q��ֵ��ʹ�õ�p��x��qʱ��P��y��![]() ��
��
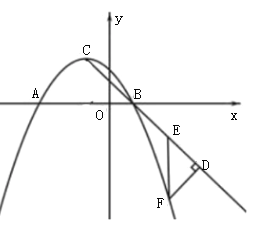
���𰸡���1������C��-1��2������2��F��3��-6������3��p=-2-![]() ��q=-2��p=0,q=1
��q=-2��p=0,q=1
��������
��1�����ݴ���ϵ����������ý���ʽ���ѽ���ʽ���ɶ���ʽ������ö������ꣻ
��2������C��![]() ���ڵ�H,���ݹ��ɶ������
���ڵ�H,���ݹ��ɶ������![]() ����ƽ���Լ�����ֱ�������ε����ʵõ�
����ƽ���Լ�����ֱ�������ε����ʵõ�![]() ���ݹ��ɶ������
���ݹ��ɶ������![]() ֤��
֤��![]() �����F
�����F![]() ����
����![]() ��
��![]() �г����̼������
�г����̼������![]() ��ֵ���������.
��ֵ���������.
��3���֢ٵ�![]() ʱ�� �ڵ�
ʱ�� �ڵ�![]() ʱ���۵�
ʱ���۵�![]() ʱ���������������.
ʱ���������������.
(1)��������![]() ������A(3,0)��B(1,0)��
������A(3,0)��B(1,0)��
��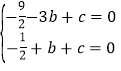 ���
���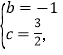
�������ߵĽ���ʽΪ![]()
��![]()
�ඥ��C������Ϊ(1,2)��
(2)��ͼ��
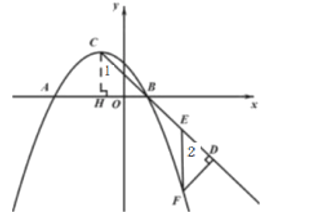
����C��![]() ���ڵ�H,
���ڵ�H,
![]()
![]()
![]()
![]()
![]()
�ڵ���ֱ��![]() �У�
�У�
![]()
![]()
![]()
![]() ��
��![]()
![]() �ɵ�ֱ��BC�Ľ���ʽΪ��
�ɵ�ֱ��BC�Ľ���ʽΪ��![]()
�����⣬���F![]() ����
����![]()
���![]()
![]()
��ã�![]() ��
��![]() ������������ȥ����
������������ȥ����
![]()
��3����![]() ʱ��
ʱ��![]()
��ã�![]()
![]()
��![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
��![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
��![]() ʱ��
ʱ��![]() �����ֵ2��
�����ֵ2��
![]() ��
��![]() ʱ��
ʱ��![]()
�����������������:
�ٵ�![]() ʱ���������Եã���
ʱ���������Եã���![]() ʱ��
ʱ��
![]() ȡ�����ֵ
ȡ�����ֵ![]()
![]() ʱ��
ʱ��![]() ����
����![]()
��ã�![]() ������������ȥ��
������������ȥ��
![]()
�ڵ�![]() ʱ����
ʱ����![]() ʱ��
ʱ��![]() ȡ�����ֵ
ȡ�����ֵ![]() ��������.
��������.
�۵�![]() ʱ���������Եã���
ʱ���������Եã���![]() ʱ��
ʱ��
![]() ȡ�����ֵ
ȡ�����ֵ![]()
![]() ʱ��
ʱ��![]() ����
����![]()
![]()
��ã�![]() ������������ȥ��
������������ȥ��
![]()
��������������������p��q��ֵΪ![]() ��
��![]()

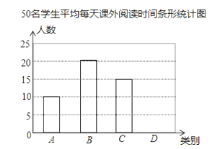
����Ŀ�������Ķ������ѧ����������Ҫ;����ijУΪ�˽�ѧ�������Ķ��������������50��ѧ����ͳ������ƽ��ÿ������Ķ�ʱ��t��Сʱ��������t�ij��̷�ΪA��B��C��D���࣬�����Ǹ����������������Ƶ�������������ͳ��ͼ���������ͼ���ṩ����Ϣ�������������⣺
50��ѧ��ƽ��ÿ������Ķ�ʱ��ͳ�Ʊ�
��� | ʱ��t��Сʱ�� | ���� |
A | t��0.5 | 10 |
B | 0.5��t��1 | 20 |
C | 1��t��1.5 | 15 |
D | t��1.5 | a |
��1�����ε������������Ϊ���٣�
��2��������е�a��ֵ������ͼ�в�ȫ����ͳ��ͼ��
��3����У����1200��ѧ����������Ƹ�У���ж�����ѧ�������Ķ�ʱ�䲻����1Сʱ��
����Ŀ���ڿ����ϣ���ʦ������ɫ�ⶼ��ͬ��1����������ɸ��������һ�������Ŀڴ������ȣ���ȫ��ͬѧ���ν����������飬ÿ���������һ��������ɫ�ٷŻؽ��ȣ��±�������õ���һ�����ݣ�
����Ĵ���n | 100 | 150 | 200 | 500 | 800 |
��������Ĵ���m | 26 | 37 | 49 | 124 | 200 |
���������Ƶ�� |
|
|
|
| a |
![]() ����a��ֵ����______��
����a��ֵ����______��
![]() ����ڴ��а���ĸ�����
����ڴ��а���ĸ�����
![]() �û���״ͼ���б��ķ���������������ͬѧ����������ĸ��ʣ�
�û���״ͼ���б��ķ���������������ͬѧ����������ĸ��ʣ�