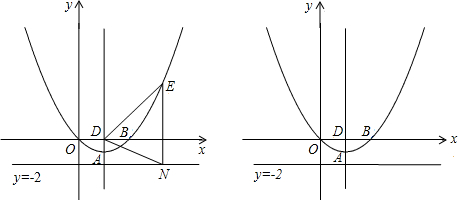题目内容
已知以A（0，2）、B（2，0）、O（0，0）三点为顶点的三角形被直线y=ax-a分成两部分．
（1）填空：不管a为何值，直线y=ax-a必过一定点C，该定点C的坐标为________．
（2）若所分的两部分的面积比为1：7，求a的值．
解：（1）令y=0，得到ax-a=0，
解得x=1，
∴C点的坐标为（1，0）；（3分）
（2）分两种情况：
①当直线y=ax-a与y轴交于点D时，
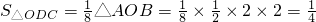．而OC=1，
所以点D的坐标为
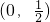，（6分）将点D的坐标代入y=ax-a中，得
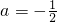．（9分）②过点D作x轴的平行线，交AB于点E，作直线CE．
因为△CEB和△ODC的面积相等，因此直线CE也是符合条件的直线．
因为直线AB的解析式为y=-x+2，
所以点E的坐标为
．（12分）将点E的坐标代入y=ax-a中，得a=1．
综上所述，
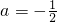或a=1（15分）分析：（1）令y=ax-a=0，解得x=1，故可以得到C点的坐标；
（2）分当直线y=ax-a与y轴交于点D时与过点D作x轴的平行线，交AB于点E，作直线CE两种情况讨论分别求得a的值即可．
点评：本题考查了一次函数的综合题，特别是第（2）问注意分两种情况讨论，漏掉另外一种情况是解决本题的易错点．
练习册系列答案
相关题目
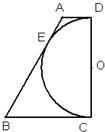6、如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切，切点分别是D，C，E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是（ ）