题目内容
【题目】学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体．不分年级、由兴趣爱好相近的同学组成，在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动．某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类)，绘制了如图所示的两幅统计图(不完整)．
请根据图中信息，解答下列问题：
(1)求扇形统计图中m的值，并补全条形统计图；
(2)已知该校有1200名学生，请估计“文学社团”共有多少人？
(3)在“动漫社团”活动中，甲、乙、丙、丁、戊五名同学表现优秀，现决定从这五名同学中任选两名参加“中学生原创动漫大赛”，请用列表或画树状图的方法求出恰好选中甲、乙两位同学的概率．
【答案】（1）m=20，补图见解析；（2）300人；（3）
【解析】
（1）用C类别人数除以其占总人数的比例可得总人数，再求出A类别的人数，由A的人数可得其所占百分比，根据A类别的人数即可补全条形图；
（2）根据样本中“文学社团”的人数所占的比例，用样本估计总体的方法即可解答；
（3）首先根据题意列出表格，再从中找到符合条件的结果数，利用概率公式计算可得．
解：（1）本次调查的总人数为15÷25%＝60（人），
∴A类别人数为：60﹣（24+15+9）＝12，
则m%＝
×100%＝20%，
补全图形如下：
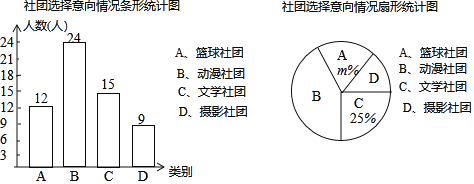
（2）估计“文学社团”共有1200×25%＝300（人）；
（3）列表得：
甲 | 乙 | 丙 | 丁 | 戊 | |
甲 | （甲，乙） | （甲，丙） | （甲，丁） | （甲，戊） | |
乙 | （乙，甲） | （乙，丙） | （乙，丁） | （乙，戊） | |
丙 | （丙，甲） | （丙，乙） | （丙，丁） | （丙，戊） | |
丁 | （丁，甲） | （丁，乙） | （丁，丙） | （丁，戊） | |
戊 | （戊，甲） | （戊，乙） | （戊，丙） | （戊，丁） |
∵共有20种等可能的结果，恰好选中甲、乙两位同学的有2种情况，
∴恰好选中甲、乙两位同学的概率为
＝．
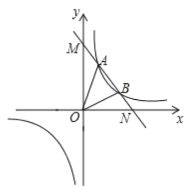
【题目】如图，一次函数
与反比例函数
的图象交于点A(
)、
两点，与坐标轴分别交于M、N两点．
（1）求一次函数的解析式；
（2）根据图象直接写出
中
的取值范围是____________；
（3）求△ABC的面积．
【题目】一汽车租赁公司拥有某种型号的汽车100辆．公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系：
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
（1）观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y（辆）与每辆车的月租金x（元）之间的关系式.
（2）已知租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．用含x（x≥3000）的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
（3）若你是该公司的经理，你会将每辆车的月租金定为多少元，才能使公司获得最大月收益？请求出公司的最大月收益是多少元．
