题目内容
【题目】一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,⊙A与水平地面切于点D,AE∥DN,某一时刻,点B距离水平面38cm,点C距离水平面59cm. 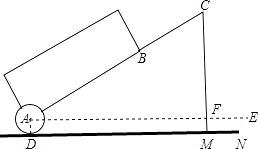
(1)求圆形滚轮的半径AD的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面73.5cm,求此时拉杆箱与水平面AE所成角∠CAE的大小(精确到1°,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
【答案】
(1)解:作BH⊥AF于点G,交DM于点H.
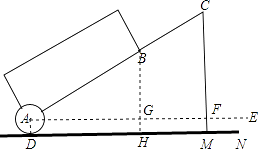
则BG∥CF,△ABG∽△ACF.
设圆形滚轮的半径AD的长是xcm.
则 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:x=8.
则圆形滚轮的半径AD的长是8cm
(2)解:CF=73.5﹣8=65.5(m).
则sin∠CAF= ![]() =
= ![]() ≈0.77,
≈0.77,
则∠CAF=50°
【解析】(1)作BH⊥AF于点G,交DM于点H,则△ABG∽△ACF,设圆形滚轮的半径AD的长是xcm,根据相似三角形的对应边的比相等,即可列方程求得x的值;(2)求得CF的长,然后在直角△ACF中,求得sin∠CAF,即可求得角的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目