题目内容
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB,AC⊥BC,那么下列结论不正确的是( )
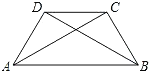
A. AC=2CD B. DB⊥AD C. ∠ABC=60° D. ∠DAC=∠CAB
【答案】A
【解析】A、根据三角形的三边关系即可得出A不正确;B、通过等腰梯形的性质结合全等三角形的判定与性质即可得出∠ADB=90°,从而得出B正确;C、由梯形的性质得出AB∥CD,结合角的计算即可得出∠ABC=60°,即C正确;D、由平行线的性质结合等腰三角形的性质即可得出∠DAC=∠CAB,即D正确.综上即可得出结论.
解:A、∵AD=DC,
∴AC<AD+DC=2CD,A不正确;
B、∵在梯形ABCD中,AD=CB,
∴梯形ABCD为等腰梯形,
∴∠DAB=∠CBA.
在△DAB和△CBA中,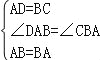 ,
,
∴△DAB≌△CBA(SAS),
∴∠ADB=∠BCA.
∵AC⊥BC,
∴∠ADB=∠BCA=90°,
∴DB⊥AD,B成立;
C、∵AB∥CD,
∴∠CDB=∠ABD,∠ABC+∠DCB=180°,
∵DC=CB,
∴∠CDB=∠CBD=∠ABD,
∵∠ACB=90°,
∴∠CDB=∠CBD=∠ABD=30°,
∴∠ABC=∠ABD+∠CBD=60°,C正确;
D、∵AB∥CD,
∴∠DCA=∠CAB,
∵AD=DC,
∴∠DAC=∠DCA=∠CAB,D正确.
故选A.
“点睛”本题考查了梯形的性质、平行线的性质、等腰三角形的性质以及全等三角形的判定与性质,解题的关键是逐项分析四个选项的正误.本题属于中档题,稍显繁琐,但好在该题为选择题,只需由三角形的三边关系得出A不正确即可.

练习册系列答案
相关题目