题目内容
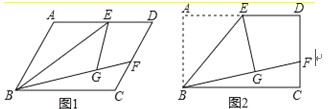
【题目】如图1,ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且 点G在□ABCD内部.将BG延长交DC于点F.
(1)猜想并填空:GF DF(填“>”、“<”、“=”);
(2)请证明你的猜想;
(3)如图2,当∠A=90°,设BG=a,GF=b,EG=c,证明:c2=ab.
【答案】(1)=;(2)证明见解析;(3)证明见解析.
【解析】(1)GF=DF,
故答案为:=;
(2)理由是:
连接DG,
由折叠得:AE=EG,∠A=∠BGE,
∵E在AD的中点,
∴AE=ED,
∴ED=EG,
∵∠EGD=∠EDG,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠BGE+∠EGF=180°,
∴∠EDF=∠EGF,
∴∠EDF﹣∠EDG=∠EGF﹣∠EGD,
即∠GDF=∠DGF,
∴GF=DF;
(3)证明:如题图2,由(2)得:DF=GF=b,
由图可得:BF=BG+GF=a+b,
由折叠可得:AB=BG=a,AE=EG=c,
在平行四边形ABCD中,
BC=AD=2AE=2c,CD=AB=a,
∴CF=CD﹣DF=a﹣b,
∵∠A=90°,
∴□ABCD是矩形,
∴∠C=90°,
在Rt△BCF中,由勾股定理得,
BC2+CF2=BF2,
∴(2c)2+(a﹣b)2=(a+b)2,
整理得:c2=ab.


练习册系列答案
相关题目