题目内容
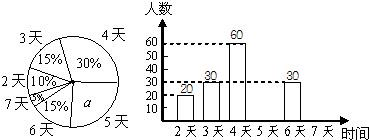
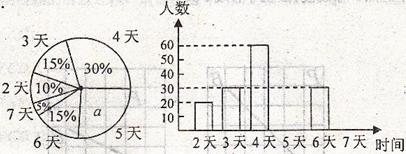
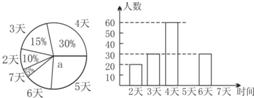
某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题: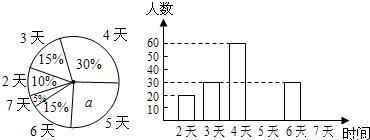
(1)求出扇形统计图中a的值,并求出该校初一学生总数;
(2)分别求出活动时间为5天、7天的学生人数,并补全频数分布直方图;
(3)求出扇形统计图中“活动时间为4天”的扇形所对圆心角的度数;
(4)在这次抽样调查中,众数和中位数分别是多少?
(5)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
【答案】分析:(1)用1减去其它5个的百分比得到a的值;通过时间为2天的人数和它占的百分比可求出总人数.
(2)通过它们所占的百分比和总人数即可求得;并且可补全频数分布直方图.
(3)用360度×30%得到.
(4)根据中位数和众数的定义解答.
(5)用样本估计总体.
解答: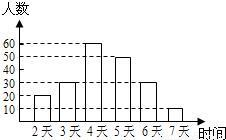 解:(1)a=1-(10%+15%+30%+15%+5%)=25%,
解:(1)a=1-(10%+15%+30%+15%+5%)=25%,
初一学生总数:20÷10%=200人;
(2)活动时间为5天的学生数:200×25%=50人,
活动时间为7天的学生数:200×5%=10人;
频数分布直方图如图:
(3)活动时间为4天的扇形所对的圆心角是360°×30%=108°;
(4)众数是4天,中位数是4天;
(5)该市活动时间不少于4天的人数约是6000×(30%+25%+15%+5%)=4500人.
点评:本题考查条形统计图、扇形统计图等知识.结合生活实际,绘制条形统计图,扇形统计图或从统计图中获取有用的信息,是近年中考的热点.只要能认真准确读图,并作简单的计算,一般难度不大.
(2)通过它们所占的百分比和总人数即可求得;并且可补全频数分布直方图.
(3)用360度×30%得到.
(4)根据中位数和众数的定义解答.
(5)用样本估计总体.
解答:
 解:(1)a=1-(10%+15%+30%+15%+5%)=25%,
解:(1)a=1-(10%+15%+30%+15%+5%)=25%,初一学生总数:20÷10%=200人;
(2)活动时间为5天的学生数:200×25%=50人,
活动时间为7天的学生数:200×5%=10人;
频数分布直方图如图:
(3)活动时间为4天的扇形所对的圆心角是360°×30%=108°;
(4)众数是4天,中位数是4天;
(5)该市活动时间不少于4天的人数约是6000×(30%+25%+15%+5%)=4500人.
点评:本题考查条形统计图、扇形统计图等知识.结合生活实际,绘制条形统计图,扇形统计图或从统计图中获取有用的信息,是近年中考的热点.只要能认真准确读图,并作简单的计算,一般难度不大.

练习册系列答案
相关题目
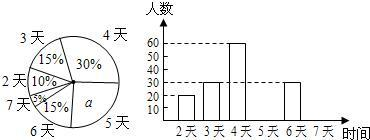 24、某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
24、某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题: