题目内容
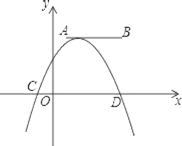
【题目】已知,抛物线ymx22mx3m(m>0),与x轴交于A、B两点(A在B的左边),与y轴交于C点.M为抛物线的顶点.
(1)求A、B两点的坐标.
(2)当m=1时,抛物线BM段有点P(不与M重合),使得SPBCSMBC.求P点的坐标.
(3)当m=1时,抛物线上有点N,使得∠NCA=2∠BCA.求N点的坐标.
【答案】(1)A(-1,0),B(3,0);(2)P(2,-3);(3)![]() .
.
【解析】
(1)令y=0,代入ymx22mx3m(m>0),即可得到答案;
(2)先求出B,M,C的坐标,由SPBCSMBC,得MP∥BC,用待定系数法,求出直线BC的解析式和直线MP的解析式,结合yx22x3,联立得到方程组,进而即可得到答案;
(3)作点A关于BC的对称点H,连接BH,CH,设CH交抛物线于点N,此时,∠NCA=2∠BCA,求出A,B,C的坐标,易得∠ABH=90°,AB=HB=4,从而得点H的坐标,进而得直线CH的函数解析式,结合yx22x3,联立得到方程组,进而即可得到答案.
(1)令y=0,代入ymx22mx3m(m>0),得:mx22mx3m=0,解得:![]() ,
,
∵抛物线ymx22mx3m(m>0),与x轴交于A、B两点(A在B的左边),
∴A(-1,0),B(3,0);
(2)∵当m=1时,抛物线yx22x3,
∴B(3,0),M(1,-4),C(0,-3),
∵SPBCSMBC,
∴点M到BC的距离与点P到BC的距离相等,即MP∥BC,
设直线BC的解析式为:y=kx+b,
把B(3,0), C(0,-3)代入上式得:![]() ,解得:
,解得:![]() ,
,
∴直线BC的解析式为:y=x-3,
设直线MP的解析式为:y=x+m,
把M(1,-4)代入上式,得-4=1+m,解得:m=-5,
∴直线MP的解析式为:y=x-5,
又∵点P在抛物线BM段,
∴联立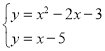 ,解得:
,解得:![]() ,
,
∴P(2,-3);
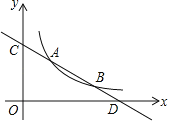
(3)作点A关于BC的对称点H,连接BH,CH,设CH交抛物线于点N,此时,∠NCA=2∠BCA,
∵当m=1时,抛物线yx22x3,
∴A(-1,0),B(3,0), C(0,-3),
∴OB=OC=3,
∴∠ABC=∠HBC=45°,
∴∠ABH=90°,
∵AB=HB=4,
∴H(3,-4),
设直线CH的解析式为:y=kx+b,
把C(0,-3),H(3,-4)代入上式得:![]() ,解得:
,解得: ,
,
∴直线CH的解析式为:y=![]() x-3,
x-3,
联立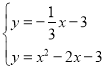 ,解得:
,解得: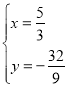 ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案