Question

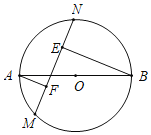
【题目】如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，顶点为D．

（1）求此抛物线的函数表达式；

（2）以点B为直角顶点作直角三角形BCE，斜边CE与抛物线交于点P，且CP＝EP，求点P的坐标；

（3）△BOC绕着它的顶点B顺时针在第一象限内旋转，旋转的角度为α，旋转后的图形为△BO1C1．当旋转后的△BO1C1有一边在直线BD上时，求△BO1C1不在BD上的顶点的坐标．

Answer 1

【答案】（1）y＝﹣x2+2x+3；（2）P为（ ）或（）；（2）C1的坐标为（3+）．

【解析】

（1）将A、B两点的坐标代入抛物线y＝﹣x2+bx+c，即可求b、c的值；

（2）过点P作PH⊥x轴于H，PG⊥y轴于G，连接PB，由条件可证得PC＝PE＝PB，证明△PCG≌△PBH，得出PG＝PH，则P点坐标易求；

（3）有两种可能：当BC1在直线BD上时，过点O1作O1M⊥OB，证明△MBO1∽△CBD，得出比例线段可求出BM、O1M的长，则点O1的坐标可求出；当BO1与BD重合时，过点B作x轴的垂线BN，过点C1作C1N⊥BN于点N，易证△NBC1∽△CBD，可求出BN、NC1的长，则C1的坐标可求出．

（1）把A（﹣1，0），B（3，0）两点代入y＝﹣x2+bx+c，

得：，

解得b＝2，c＝3，

∴抛物线的函数表达式为y＝﹣x2+2x+3；

（2）如图1，（2）过点P作PH⊥x轴于H，PG⊥y轴于G，连接PB，

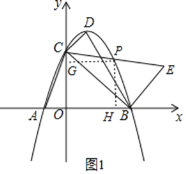
设P（m，﹣m2+2m+3），易知C（0，3），

∵OC＝OB，

∴∠OCB＝∠OBC＝45°，

∵PC＝PB，

∴∠PBC＝∠PCB，

∴∠PCG＝∠PBC，

又∵PC＝PB，

∴Rt△PCG≌Rt△PBH（AAS），

∴PG＝PH，

∴m＝﹣m2+2m+3，

解得：m＝．

∴P为（ ）或（）；

（3）如图2，当BC1在直线BD上时，过点O1作O1M⊥OB，由y＝﹣x2+2x+3可得D（1，4）．

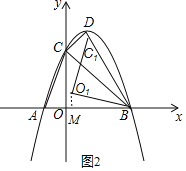
∴DC＝，BC＝3，DB＝2，

∴DC2+BC2＝BD2，

∴△BCD为直角三角形，且∠BCD＝90°，

∵∠DBC+∠CBO1＝∠CBO1+∠ABO1＝45°，

∴∠ABO1＝∠DBC，

∴△MBO1∽△CBD，

∴，

即，

∴，，

∴点O1的坐标为（），

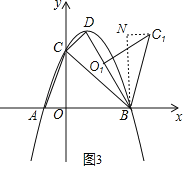
如图3，当BO1与BD重合时，过点B作x轴的垂线BN，过点C1作C1N⊥BN于点N，

易证△NBC1∽△CBD，

∴，

∴，

∴，则C1的坐标为（）．