题目内容
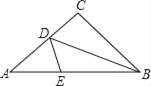
【题目】(情境)某课外兴趣小组在一次折纸活动课中.折叠一张带有条格的长方形的纸片ABCD(如图1),将点B分别与点A,A1,A2,…,D重合,然后用笔分别描出每条折痕与对应条格线所在的直线的交点,用平滑的曲线顺次连结各交点,得到一条曲线.
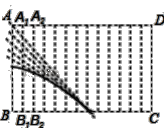
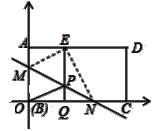
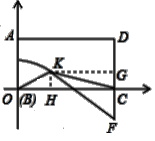
图1 图2 图3
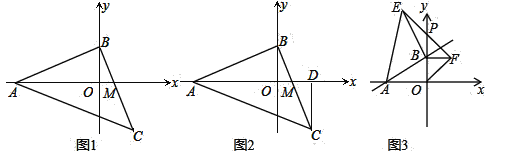
(探索)(1)如图2,在平面直角坐标系xOy中,将矩形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB边放在y轴的正半轴上,AB=m,AD=n,(m≤n).将纸片折叠,使点B落在边AD上的点E处,过点E作EQ⊥BC于点Q,折痕MN所在直线与直线EQ相交于点P,连结OP.求证:四边形OMEP是菱形;
(归纳)(2)设点P坐标是(x,y),求y与x的函数关系式(用含m的代数式表示).
(运用)(3)将矩形纸片ABCD如图3放置,AB=8,AD=12,将纸片折叠,当点B与点D重合时,折痕与DC的延长线交于点F.试问在这条折叠曲线上是否存在点K,使得△KCF的面积是△KOC面积的![]() ?若存在,写出点K的坐标;若不存在,请说明理由.
?若存在,写出点K的坐标;若不存在,请说明理由.
【答案】(1)见解析 (2)y=![]() (3)点K(2+2
(3)点K(2+2![]() ,
,![]() )
)
【解析】(1)、如果四边形的四边相等,那么这个四边形是菱形;(2)、根据P点的坐标,可表示出E点的坐标,从而可知道OP的长,用勾股定理表示出解析式;(3)、首先画出图形,作KG⊥DC于G,KH⊥OC于H.设K(x,y),根据面积的关系得出y=![]() ,将点K的坐标代入二次函数解析式,从而得出x的值,得出点K的坐标.
,将点K的坐标代入二次函数解析式,从而得出x的值,得出点K的坐标.
(1)、证明:如图3,由题意知:OM=ME,∠OMN=∠EMN, ∵OM∥EP,∴∠OMN=∠MPE.
∴∠EMN=∠MPE. ∴ME=EP.∴OM=EP. ∴四边形OMEP是平行四边形.
又∵ME=EP,∴四边形OMEP是菱形;
(2)、解:∵四边形OMEP是菱形, ∴OP=PE,∴OP2=PE2, ∵EQ=OA=m,PQ=y,
∴PE=m﹣y.∴PE2=(m﹣y)2=m2﹣2my+y2.
∵OP2=x2+y2,PE2=m2﹣2my+y2, ∴x2+y2=m2﹣2my+y2. ∴y=![]() ;
;
(3)、解:如图3,假设折叠曲线上存在点K满足条件.
当m=8时,y=﹣![]() x2+4. 作KG⊥DC于G,KH⊥OC于H.设K(x,y),
x2+4. 作KG⊥DC于G,KH⊥OC于H.设K(x,y),
则KG=12﹣x,KH=y. 当x=12时,y=﹣5. ∴F(12,﹣5), ∴CF=5.
∴S△KCF=![]() CF×KG=
CF×KG=![]() ×5×(12﹣x), S△KOC=
×5×(12﹣x), S△KOC=![]() CO×KH=
CO×KH=![]() ×12y, ∵S△KCF=
×12y, ∵S△KCF=![]() S△KOC,
S△KOC,
∴0.5×5·(12-x)=![]() ×
×![]() ×12·y ∴y=
×12·y ∴y=![]() . ∴K(x,
. ∴K(x,![]() ).
).
∵点K在y=﹣![]() x2+4上, ∴
x2+4上, ∴![]() =﹣
=﹣![]() x2+4. 化简得:x2﹣4x﹣16=0,
x2+4. 化简得:x2﹣4x﹣16=0,
解得:x1=2+2![]() ,x2=2﹣2
,x2=2﹣2![]() (舍去), 当x1=2+2
(舍去), 当x1=2+2![]() 时,y=
时,y=![]() ,
,
∴存在点K(2+2![]() ,
,![]() ).
).

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案