��Ŀ����
����Ŀ����ͼ��������y=ax2+bx��4��x�ύ��A����2��0����B��8��0�����㣬��y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��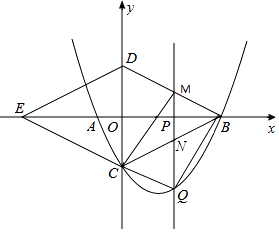
��1���������ߵĽ���ʽ��
��2������P���߶�OB���˶�ʱ��ֱ��l�ֱ�BD��BC�ڵ�M��N����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���ʱ�����ж��ı���CQBM����״����˵�����ɣ�
��3������P���߶�EB���˶�ʱ���Ƿ���ڵ�Q��ʹ��BDQΪֱ�������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��x=0����ã�y=��4��
��C��0����4����
�������ߵĽ���ʽΪy=a��x+2����x��8��������C���������ã���16a=��4����ã�a= ![]() ��
��
�������ߵĽ���ʽΪy= ![]() ��x+2����x��8����y=
��x+2����x��8����y= ![]() x2��
x2�� ![]() x��4��
x��4��
��2���⣺�����εĶԳ��Կ�֪����D������Ϊ��0��4����
��ֱ��BD�Ľ���ʽΪy=kx+4������B���������ã�8k+4=0����ã�k=�� ![]() ��
��
��ֱ��BD�Ľ���ʽΪy=�� ![]() x+4��
x+4��
��l��x�ᣬ
���M��Q������ֱ��ǣ�m���� ![]() m+4������m��
m+4������m�� ![]() m2��
m2�� ![]() m��4����
m��4����
��MQ=DCʱ���ı���CQMDΪƽ���ı��Σ�
�ࣨ�� ![]() m+4������
m+4������ ![]() m2��
m2�� ![]() m��4��=8������ã�m2��4m=0�����m=4��m=0����ȥ����
m��4��=8������ã�m2��4m=0�����m=4��m=0����ȥ����
��ʱ���ı���CQBM��ƽ���ı��Σ�
���ı���CQBMΪƽ���ı��Σ�
��MD��CQ��MD=CQ��
��m=4ʱ��M������Ϊ��4��2����
��MΪBD���е㣬
��MD=MB��
��CQ=MB��
�֡�MB��CQ��
���ı���CQBMΪƽ���ı��Σ�
��3���⣺��QB�Ľ���ʽΪy=k1x+b1������B�͵�Q���������ã� 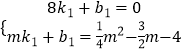 ��
��
��ã�k1= ![]() =
= ![]() ��m+2����
��m+2����
��QD�Ľ���ʽΪy=k2x+4������Q����������mk2+4= ![]() m2��
m2�� ![]() m��4��
m��4��
��ã�k2= ![]() ��
��
����QBD=90��ʱ���� ![]() ��
�� ![]() ��m+2��=��1����ã�m=6��
��m+2��=��1����ã�m=6��
��Q��6����4����
����QDB=90��ʱ���� ![]() ��
�� ![]() =��1�������ã�m2��14m��32=0�����m=��2��m=16����ȥ����
=��1�������ã�m2��14m��32=0�����m=��2��m=16����ȥ����
��Q����2��0����
��MΪԲ����MBΪ�뾶����M����M��������û�й����㣬
���DQB��90�㣮
������������Q��������6����4����2��0����
����������1�����ô���ϵ��������A��B��������������ʽ�����a��b���ɣ���2��Ҫʹ�ı���CQMD��ƽ���ı��Σ���MQ=DC=8�������� ![]() m+4������
m+4������ ![]() m2��
m2�� ![]() m��4��=8���������̣������m;��3������BDQΪֱ�������Σ���������ۣ���QBD=90����QDB=90�㣬������ֱ�ߵ�б�ʻ�Ϊ-1��������m�ķ��̣����m,����MΪԲ����MBΪ�뾶����M����M��������û�й����㣬��ˡ�DQB��90��.
m��4��=8���������̣������m;��3������BDQΪֱ�������Σ���������ۣ���QBD=90����QDB=90�㣬������ֱ�ߵ�б�ʻ�Ϊ-1��������m�ķ��̣����m,����MΪԲ����MBΪ�뾶����M����M��������û�й����㣬��ˡ�DQB��90��.

 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�