��Ŀ����
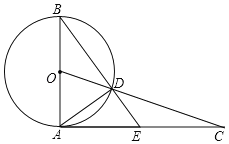
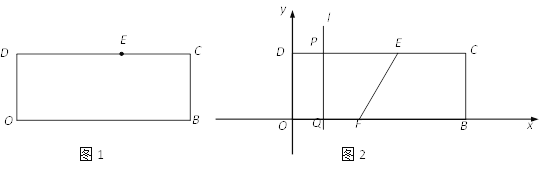
����Ŀ�����壺���һ�����������������㹹��ֱ�������Σ���������Ϊ����������Ĺ��ɵ㣮�����OBCD�У���CΪO��B����Ĺ��ɵ�,��֪OD��4,��DC��ȡ��E,DE=8��
��1�������E��O��B����Ĺ��ɵ㣨��E���ڵ�C��, ����OB�ij���
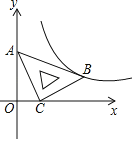
��2�����OB=12���ֱ���OB,ODΪ�����Ὠ����ͼ2��ֱ������ϵ����x����ȡ��F(5��0)�����߶�DC��ȡ��P, ����P��ֱ��l��y�ᣬ��x���ڵ�Q����DP=t��
������P��DE֮�䣬��EFΪֱ����Բ��ֱ��l���У�����t��ֵ��
����ֱ��l��ǡ����2����E��F����Ĺ��ɵ�ʱ��������Ӧt��ȡֵ��Χ��
���𰸡���1��10����2����4����0��t��4��t=5��t=8��9��t��12
��������
��1������OE��BE����OB=x����EC=x-8�������ݹ��ɶ�����ʾ��OE2��BE2��ֵ�������ݹ��ɶ������涨���з�����⼴�ɣ�
��2���ٹ���F��FG��DC������ΪG������M��MN��DE������EFG�����ݹ��ɶ������EF�ij����Ӷ������MH�ij��������ε���λ�߶��������MN�ij���Ȼ������NH=NM-MH�����NH�ij����Ӷ����t��ֵ��
�ڵ�ֱ��l��ԲM�����ֱ��l������E��ֱ��l������Fʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
�⣺��1����ͼ1��ʾ������OE��BE��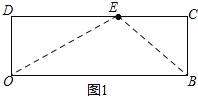
��OB=x����EC=x-8��
����DOE��OE2=DE2+OD2=42+82=80��BE2=CE2+CB2=42+��x-8��2��
��EΪ��O�͵�B�Ĺ��ɶ����㣬
��OB2=OE2+BE2����42+��x-8��2+80=x2��
��ã�x=10��
��OB=10��
��2���ٹ���F��FG��DC������ΪG������M��MN��DE��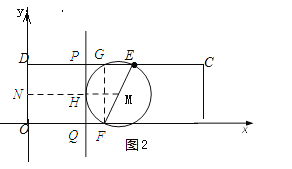
��DE=8��OF=5��DO=4��
��GE=3��FG=4��MN=6.5��
��EF=![]() =5��
=5��
��MH=2.5��
��HN=NM-MH=6.5-2.5=4��
��t=4��
����ͼ3��ʾ����ֱ��l��ԲM����ʱ������E��EG��EF��PQ�ڵ�G������F��HF��EF������ΪH��
�ߡ�GEF=90����
���GEFΪֱ�������Σ�
��G��E��F��һ�����ɵ㣮
ͬ����HҲ��E��F��һ�����ɵ㣮
�൱ֱ��l��ԲM����ʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
�൱0��t��4ʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
ͬ������ֱ��l��ԲM���Ҳֱ࣬��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
��9��t��12��
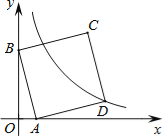
��ͼ4��ʾ����ֱ��l������Fʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮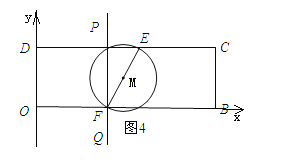
��OF=5��
��t=5��
��ͼ5��ʾ����ֱ��l������Eʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
��DE=8��
��t=8��
����������0��t��4��t=5��t=8��9��t��12ʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮