Question

如图：已知OD、OE、OF分别为∠AOB、∠AOC、∠BOC的平分线，则∠DOE和∠BOF有怎样的关系？说明理由．

Answer 1

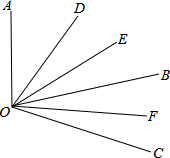
答：∠DOE=∠BOF．
理由：∵OD、OE、OF分别为∠AOB、∠AOC、∠BOC的平分线，
∴∠AOE=

1

2

∠AOC，∠AOD=

1

2

∠AOB，∠BOF=

1

2

∠BOC，
∴∠DOE=∠AOE-∠AOD=

1

2

（∠AOC-AOB），
∵∠AOB+∠BOC=∠AOC，
∴∠DOE=∠AOE-∠AOD=

1

2

∠BOC，
∴∠DOE=∠BOF．