题目内容
(2012•海淀区一模)已知关于x的方程 mx2+(3m+1)x+3=0.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)若抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,试确定此抛物线的解析式;
(3)若点P(x1,y1)与Q(x1+n,y2)在(2)中抛物线上 (点P、Q不重合),且y1=y2,求代数式4x12+12x1n+5n2+16n+8的值.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)若抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,试确定此抛物线的解析式;
(3)若点P(x1,y1)与Q(x1+n,y2)在(2)中抛物线上 (点P、Q不重合),且y1=y2,求代数式4x12+12x1n+5n2+16n+8的值.
分析:(1)分别讨论当m=0和m≠0的两种情况,分别对一元一次方程和一元二次方程的根进行判断;
(2)令y=0,则 mx2+(3m+1)x+3=0,求出两根,再根据抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,求出m的值;
(3)点P(x1,y1)与Q(x1+n,y2)在抛物线上,求出y1和y2,y1和y2相等,求出 n(2x1+n+4)=0,然后整体代入求出代数式的值.
(2)令y=0,则 mx2+(3m+1)x+3=0,求出两根,再根据抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,求出m的值;
(3)点P(x1,y1)与Q(x1+n,y2)在抛物线上,求出y1和y2,y1和y2相等,求出 n(2x1+n+4)=0,然后整体代入求出代数式的值.
解答:解:(1)当m=0时,原方程化为x+3=0,此时方程有实数根 x=-3.
当m≠0时,原方程为一元二次方程.
∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2≥0.
∴此时方程有两个实数根.
综上,不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根.
(2)∵令y=0,则 mx2+(3m+1)x+3=0.
解得 x1=-3,x2=-
.
∵抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,
∴m=1.
∴抛物线的解析式为y=x2+4x+3.
(3)∵点P(x1,y1)与Q(x1+n,y2)在抛物线上,
∴y1=x12+4x1+3,y2=(x1+n)2+4(x1+n)+3.
∵y1=y2,
∴x12+4x1+3=(x1+n)2+4(x1+n)+3.
可得 2x1n+n2+4n=0.
即 n(2x1+n+4)=0.
∵点P,Q不重合,
∴n≠0.
∴2x1=-n-4.
∴4
+12x1n+5n2+16n+8=(2x1)2+2x1•6n+5n2+16n+8=(n+4)2+6n(-n-4)+5n2+16n+8=24.
当m≠0时,原方程为一元二次方程.
∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2≥0.
∴此时方程有两个实数根.
综上,不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根.
(2)∵令y=0,则 mx2+(3m+1)x+3=0.
解得 x1=-3,x2=-
| 1 |
| m |
∵抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,
∴m=1.
∴抛物线的解析式为y=x2+4x+3.
(3)∵点P(x1,y1)与Q(x1+n,y2)在抛物线上,
∴y1=x12+4x1+3,y2=(x1+n)2+4(x1+n)+3.
∵y1=y2,
∴x12+4x1+3=(x1+n)2+4(x1+n)+3.
可得 2x1n+n2+4n=0.
即 n(2x1+n+4)=0.
∵点P,Q不重合,
∴n≠0.
∴2x1=-n-4.
∴4
| x | 2 1 |
点评:本题主要考查二次函数的综合题的知识,解答本题的关键熟练掌握方程与函数之间的联系,此题难度不大,第三问需要整体代入.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 (2012•海淀区一模)如图,在△ABC中,∠C=90°,点D在CB上,DE⊥AB,若DE=2,CA=4,则
(2012•海淀区一模)如图,在△ABC中,∠C=90°,点D在CB上,DE⊥AB,若DE=2,CA=4,则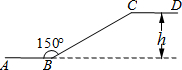 (2012•海淀区一模)如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为
(2012•海淀区一模)如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为