题目内容
已知⊙O的半径为5cm，A是⊙O内一点，AO=3cm，那么过点A最短的弦长为
8
8
cm．分析：当过A的弦与OA垂直时，此时的弦长最短，连接OC，利用垂径定理得到A为AB的中点，在直角三角形AOC中，由OA与OC的长，利用勾股定理求出AC的长，由BC=2AC即可求出BC的长．
解答：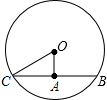
解：如图，当过A的弦与OA垂直时，此时的弦长最短，连接OC，
利用垂径定理得到P为AB的中点，即AC=
BC，
在Rt△AOP中，OA=3cm，OC=5cm，
根据勾股定理得：AC=
=4cm，
则过点A最短的弦长BC=8cm．
故答案是：8．
解：如图，当过A的弦与OA垂直时，此时的弦长最短，连接OC，利用垂径定理得到P为AB的中点，即AC=
| 1 |
| 2 |
在Rt△AOP中，OA=3cm，OC=5cm，
根据勾股定理得：AC=
| OC2-OA2 |
则过点A最短的弦长BC=8cm．
故答案是：8．
点评：此题考查了垂径定理，以及勾股定理，熟练掌握垂径定理是解本题的关键．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
如图，已知⊙O的半径为5，弦AB=6，M是AB上任意一点，则线段OM的长可能是（ ）| A、2.5 | B、3.5 | C、4.5 | D、5.5 |
如图，已知⊙O的半径为5，弦AB=8，M是AB上任意一点，则线段OM的长可以是（ ）| A、1.5 | B、2.5 | C、4.5 | D、5.5 |