题目内容
(2012•鼓楼区一模)已知⊙O1的半径为2,⊙O2的半径为5,若⊙O1和⊙O2有2个公共点,则圆心距O1O2的长度可以是( )
分析:半径不相等的两个圆有2个公共点,则两圆相交,根据两圆相交时圆心距d满足的条件:R-r<d<R+r(d表示圆心距,R,r分别表示两圆的半径,其中R>r)即可求解.
解答:解:两圆半径差为5-2=3,半径和为5+2=7,
两圆相交时,圆心距大于两圆半径差,且小于两圆半径和,
所以,3<O1O2<7,符合条件的数只有B.
故选B.
两圆相交时,圆心距大于两圆半径差,且小于两圆半径和,
所以,3<O1O2<7,符合条件的数只有B.
故选B.
点评:本题考查了圆与圆的位置关系.圆和圆的位置与两圆的圆心距、半径的数量之间的关系(d表示圆心距,R,r分别表示两圆的半径):
①两圆外离?d>R+r;
②两圆外切?d=R+r;
③两圆相交?R-r<d<R+r(R≥r);
④两圆内切?d=R-r(R>r);
⑤两圆内含?d<R-r(R>r).
①两圆外离?d>R+r;
②两圆外切?d=R+r;
③两圆相交?R-r<d<R+r(R≥r);
④两圆内切?d=R-r(R>r);
⑤两圆内含?d<R-r(R>r).

练习册系列答案
相关题目
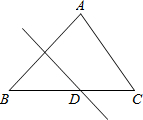 (2012•鼓楼区一模)如图,△ABC中,∠ABC=45°,AC=10,对折使点B与点A重合,折痕与BC交于点D,BD:DC=4:3,则DC的长为( )
(2012•鼓楼区一模)如图,△ABC中,∠ABC=45°,AC=10,对折使点B与点A重合,折痕与BC交于点D,BD:DC=4:3,则DC的长为( )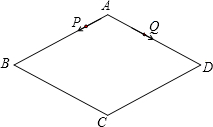 /s;点Q沿折线A-D-C-B运动,速度为1.5cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.
/s;点Q沿折线A-D-C-B运动,速度为1.5cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.