题目内容
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角形的直角顶点放在点O处, 一边OM在射线OB上,另一边ON在直线AB的下方.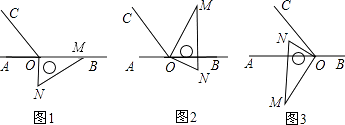
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少秒?(直接写出结果)
【答案】
(1)解:直线ON平分∠AOC,
∵∠BOC=120°,
∴∠AOC=60°,
∵OM平分∠BOC,
∴∠BOM= ![]() ∠BOC=60°,
∠BOC=60°,
∵∠MON=90°,
∴∠BON=30°,
∴直线ON平分∠AOC
(2)解:由(1)得,当直线ON旋转60°或240°时,ON平分锐角∠AOC,
∴t=10或40秒
【解析】(1)根据平角的定义求出∠AOC,根据角平分线的定义计算即可;(2)根据(1)的结论和旋转的性质解答.
【考点精析】利用角的平分线和角的运算对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.

练习册系列答案
相关题目