题目内容
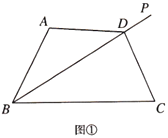
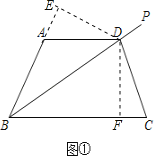
【题目】[问题]如图①,点![]() 是
是![]() 的角平分线
的角平分线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() 与
与![]() 互补,则线段
互补,则线段![]() 与
与![]() 有什么数量关系?
有什么数量关系?
[探究]
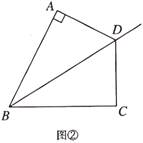
探究一:如图②,若![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,又因为
,又因为![]() 平分
平分![]() ,所以
,所以![]() ,理由是:_______.
,理由是:_______.
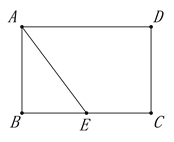
探究二:若![]() ,请借助图①,探究
,请借助图①,探究![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
[结论]点![]() 是
是![]() 的角平分线
的角平分线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() 与
与![]() 互补,则线段
互补,则线段![]() 与
与![]() 的数量关系是______.
的数量关系是______.
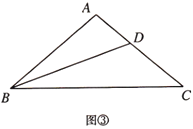
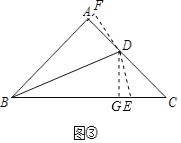
[拓展]已知:如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() .求证:
.求证:![]() .
.
【答案】探究一:角的平分线上的点到角的两边距离相等;探究二:AD=CD;理由见解析;[结论]:AD=CD;[拓展]:见解析.
【解析】
探究一:根据角平分线的性质定理解答;
探究二:作![]() 于
于![]() ,作
,作![]() 交
交![]() 的延长线于
的延长线于![]() ,证明
,证明![]() ,根据全等三角形的性质证明结论;
,根据全等三角形的性质证明结论;
[理论] 根据探究结果得到答案;
[拓展]在![]() 上取一点
上取一点![]() ,使
,使![]() ,作
,作![]() 角
角![]() 的延长线于
的延长线于![]() ,
,![]() 于
于![]() ,证明
,证明![]() ,得到
,得到![]() ,根据等腰三角形的性质得到
,根据等腰三角形的性质得到![]() ,等量代换得到
,等量代换得到![]() ,结合图形证明结论.
,结合图形证明结论.
解:探究一:![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
理由是:角平分线上的点到角的两边的距离相等,
故答案为:角平分线上的点到角的两边的距离相等;
探究二:作![]() 于
于![]() ,作
,作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
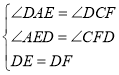 ,
,
![]()
![]() ;
;
[理论] 综上所述,点![]() 是
是![]() 的角平分线
的角平分线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() 与
与![]() 互补,则线段
互补,则线段![]() 与
与![]() 的数量关系是
的数量关系是![]() ,
,
故答案为:![]() ;
;
[拓展] 在![]() 上取一点
上取一点![]() ,使
,使![]() ,作
,作![]() 角
角![]() 的延长线于
的延长线于![]() ,
,![]() 于
于![]() ,
,
![]() .
.
![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
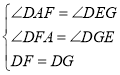 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由