Question

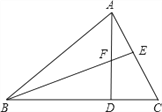
【题目】如图，AD是△ABC的高，E为AC上一点， BE交AD于F，且有DC=FD，AC=BF．

（1）说明△BFD≌△ACD；

（2）若，求AD的长；

（3）请猜想BF和AC的位置关系并说明理由.

Answer 1

【答案】（1）证明见解析；（2）AD=；（3）BF⊥AC.

【解析】试题分析：（1）在Rt△ACD和Rt△BFD中，根据直角边DC=FD和斜边AC=BF对应相等，可证明△BFD≌△ACD；

（2）由（1）知：AD=BD，又AD⊥BC，△ADB为等腰直角三角形，已知斜边AB的长，运用勾股定理可将AD的长求出；

（3）由△ADC≌△BDF，得到∠EBC=∠DAC，又因为∠DAC+∠ACD=90°，所以∠EBC+∠ACD=90°，则BE⊥AC，即BF⊥AC．

试题解析：解：（1）∵AD是ABC的高，∴△ACD与△BFD都是直角三角形，

∵DC=FD，AC=BF，∴Rt△ACD≌Rt△BFD．

（2）∵Rt△ACD≌Rt△BFD，∴AD=BD．

在Rt△ACD中，∵AD2+BD2=AB2，∴2AD2=AB2，∴AD=；

（3）∵△ADC≌△BDF，∴∠EBC=∠DAC．

又∵∠DAC+∠ACD=90°，∴∠EBC+∠ACD=90°，∴∠BEC=90°，∴BE⊥AC，即BF⊥AC．