题目内容
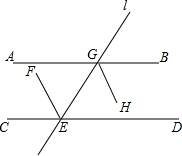 已知如图:直线AB、CD被l所截,AB∥CD,EF平分∠CEG,GH平分∠BGE.求证:EF∥GH.
已知如图:直线AB、CD被l所截,AB∥CD,EF平分∠CEG,GH平分∠BGE.求证:EF∥GH.分析:根据平行线的性质由AB∥CD得到∠CEG=∠BGE,再根据角平分线的定义得到∠FEG=
∠CEG,∠HGE=
∠BGE,则∠FEG=∠HGE,然后根据平行线的判定即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵AB∥CD,
∴∠CEG=∠BGE,
∵EF平分∠CEG,GH平分∠BGE,
∴∠FEG=
∠CEG,∠HGE=
∠BGE,
∴∠FEG=∠HGE,
∴EF∥GH.
∴∠CEG=∠BGE,
∵EF平分∠CEG,GH平分∠BGE,
∴∠FEG=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FEG=∠HGE,
∴EF∥GH.
点评:本题考查了平行线的性质与判定:两直线平行,内错角相等;内错角相等,两直线平行.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
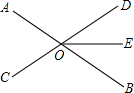 已知如图,直线AB、CD相交于O,∠AOC=50°,OE平分∠DOB,求∠COE的度数.
已知如图,直线AB、CD相交于O,∠AOC=50°,OE平分∠DOB,求∠COE的度数.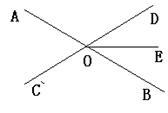
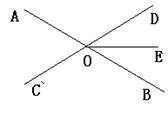
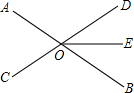 已知如图,直线AB、CD相交于O,∠AOC=50°,OE平分∠DOB,求∠COE的度数.
已知如图,直线AB、CD相交于O,∠AOC=50°,OE平分∠DOB,求∠COE的度数.