题目内容
如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.(1)若DA=
 ,求DB的长;
,求DB的长;(2)若DA、DB是方程2x2-(2k+1)x+k2-7=0的两根,求k的值;
(3)估计AB的长度的范围.
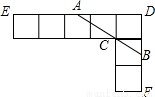
【答案】分析:(1)判断出△ACG∽△ABD,利用相似三角形的性质解答即可;
(2)直接根据根与系数的关系列出关于k的方程,解答即可;
(3)根据三角形的三边关系解答即可.
解答: 解:(1)如图,
解:(1)如图,
易得△ACG∽△ABD,
故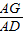 =
=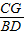 ,
,
即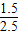 =
=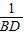 ,
,
∴BD= .
.
(2)根据根与系数的关系,DA+BD=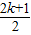 ,DA•DB=
,DA•DB=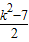
∵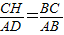 ,
,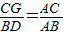
即: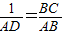 ,
,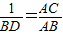
∴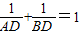
∴AD+BD=AD•BD
∴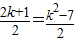
解得:k=4或-2
(3)在△ABD中, -
- <AB<
<AB< +
+ ,
,
即 <AB<
<AB<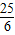 .
.
点评:此题考查了相似三角形的性质、根与系数的关系等内容,结合图形的性质解答,事半功倍.
(2)直接根据根与系数的关系列出关于k的方程,解答即可;
(3)根据三角形的三边关系解答即可.
解答:
 解:(1)如图,
解:(1)如图,易得△ACG∽△ABD,
故
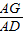 =
=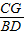 ,
,即
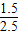 =
=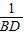 ,
,∴BD=
 .
.(2)根据根与系数的关系,DA+BD=
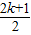 ,DA•DB=
,DA•DB=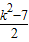
∵
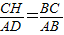 ,
,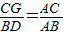
即:
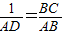 ,
,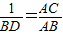
∴
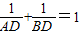
∴AD+BD=AD•BD
∴
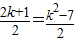
解得:k=4或-2
(3)在△ABD中,
 -
- <AB<
<AB< +
+ ,
,即
 <AB<
<AB<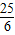 .
.点评:此题考查了相似三角形的性质、根与系数的关系等内容,结合图形的性质解答,事半功倍.

练习册系列答案
相关题目
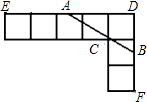 如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.
如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B. 如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.
如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.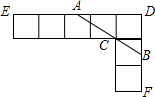 如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.
如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B. ,求DB的长;
,求DB的长; ,求DB的长;
,求DB的长;